DOI Nr.: https://doi.org/10.25929/9tgk-7r24
Harm Bandholz
UniCredit Bank AG
Jörg Clostermann
Technische Hochschule Ingolstadt
Franz Seitz
Ostbayerische Technische Hochschule
Amberg-Weiden
ABSTRACT
Seit der Finanzkrise verfolgt die US-amerikanische Notenbank (FED) einen sehr expansiven geldpolitischen Kurs. Die Zinsen wurden auf historische Niedrigstniveaus gesenkt, darüber hinaus griff die FED auf verschiedene Maßnahmen quantitativer Lockerungen zurück. Trotz dieser Ereignisse zeigen die ökonometrischen Analysen in diesem Papier, dass die klassischen Einflussfaktoren (Notenbankzinsen, Inflationserwartungen, Auslandsnachfrage nach US-Staatsanleihen) weiterhin signifikante Erklärungskraft besitzen. Allerdings sind diese Zusammenhänge in den letzten Jahren instabiler geworden. Darüber hinaus gibt es Anzeichen dafür, dass das Anleihenaufkaufprogramm der FED einen messbaren Einfluss auf die Langfristzinsen hat.
JEL Klassifikationsnummern: E43, E52, E58.
Since the financial crisis, the FED has followed an expansionary monetary policy stance. Interest rates have reached historical low levels and the FED introduced several variants of quantitative easing. Despite these actions, our econometric results show that traditional determinants of long-term interest rates (central bank rates, inflationary expectations, foreign demand for US bonds, the business cycle) still exert a significant influence. However, it turned out that the relationships have become more unstable in the last few years. Moreover, the asset purchases of the FED seem to have contributed to the low levels of long-term rates, at least partly.
KEYWORDS
Geldpolitik, USA, Finanzkrise, Staatsanleihenrendite, Federal Reserve Board, Quantitative Easing, Zinsprognose, Fehlerkorrekturmodell
Monetary policy, USA, financial crisis, government bond yield, FED, quantitative easing, interest rate forecast, error correction model
1. Einführung
Mit der Finanzkrise ist die US-amerikanische Notenbank Federal Reserve (FED) auf einen sehr expansiven geldpolitischen Kurs eingeschwenkt. Das Federal Funds Rate Target, die Zinsrate, zu der US-Banken untereinander Geld leihen, wurde bereits 2009 auf nahe 0% gesenkt; darüber hinaus griff die FED auf verschiedene Maßnahmen quantitativer Lockerungen (quantitative easing) zurück.1
Schon vor der Finanzmarktkrise waren die US-Langfristzinsen aus historischer Perspektive betrachtet sehr niedrig. Dies veranlasste Alan Greenspan, den damaligen Chairman der FED, im Februar 2005 von einem „Conundrum“ zu sprechen.2 Viele „außergewöhnliche Ursachen“ für diese Entwicklung wurden in der Folgezeit ins Feld geführt.3 Trotz der vermeintlich aus der Zinsperspektive betrachteten „schwer erklärlichen“ Situation zeigen Bandholz et. al. 2009 [1], dass man mit wenigen klassischen Determinanten (Kurzfristzins, Inflationserwartungen, Konjunktur, Auslandsnachfrage nach US-Staatspapieren) die Entwicklung der zehnjährigen Treasury Yields (US-Staatsanleiherenditen) während der Greenspan Ära (1985-2005) sehr gut erklären kann und daraus abgeleitete Zinsprognosen besser als Random-Walk-Modelle4 sind.
Vor diesem Hintergrund scheint es angebracht, das Zinsmodell von Bandholz et. al. [1] als Referenzmodell zu definieren und zu prüfen, ob es weiterhin, d. h. auch in Zeiten des quantitative easing und der Nullzinspolitik der FED, geeignet ist, die Entwicklung zu erklären und gute Prognosen für die zehnjährigen US-Staatsanleiherenditen zu generieren.
Die weiteren Ausführungen gliedern sich wie folgt: In einem ersten Schritt wird die zugrundeliegende Theorie des Modells von Bandholz et. al. [1] nachgezeichnet und das daraus folgende empirische Modell geschätzt, einmal für den von Bandholz et. al. [1] gewählten, dann für den bis zum aktuellen Rand verlängerten Zeitraum. Nach einem Vergleich der Ergebnisse erweitern wir das Modell um eine weitere Variable, die monetäre Basis. Diese Variable steht für die massive Ausweitung der Zentralbankbilanz infolge verschiedener geldpolitischer Maßnahmen der FED als Reaktion auf die Finanzkrise und deren Folgewirkungen. Auch dieses Modell wird interpretiert und seine Erklärungskraft und Prognoseperformance evaluiert. Die Arbeit endet mit einer Zusammenfassung der Ergebnisse und Schlussfolgerungen.
2. Das theoretische Modell und die Daten
Wie viele Zinsanalysen von Banken, Zentralbanken und internationalen Organisationen wie IWF, OECD oder BIZ stellen auch Bandholz et. al. [1] bezüglich der Entwicklung des US-Langfristzinses u. a. auf folgende drei Faktoren ab: Die Inflationserwartungen, den Konjunkturverlauf und die Zinspolitik der US-Notenbank. Theoretisch lässt sich die Wahl dieser drei Faktoren wie folgt begründen:
Nach der Fisher-Gleichung5 kann man den Nominalzins in den Realzins und die erwartete Inflationsrate zerlegen. Sind die Realzinsen stationär, schlagen sich die Inflationserwartungen direkt proportional in Schwankungen des Nominalzinses nieder.
Nach der „Loanable-Funds“-Theorie6 erhöht sich bei einem Konjunkturaufschwung das Angebot sowie die Nachfrage nach langfristigen Wertpapieren. Zusätzlich sinkt mit einem verbesserten konjunkturellen Umfeld die Risikoprämie dieser Wertpapiere. Ist der Nachfrageeffekt nur schwach ausgeprägt, schwanken die Renditen positiv mit der Konjunktur.
Nach der Erwartungs- und der Liquiditätsprämientheorie7 der Zinsstruktur besteht ein direkt proportionaler Zusammenhang zwischen dem aktuellen kurzfristigen und dem langfristigen Zins. Zudem postulieren diese Theorien, dass die langfristigen Zinsen den zukünftigen Pfad der kurzfristigen Zinsen widerspiegeln (gegeben die Laufzeitenprämie)8. Demnach würde man einen kausalen Zusammenhang vom aktuellen langfristigen zum aktuellen kurzfristigen Zins vermuten. Allerdings hat die Notenbank eine dominante Stellung am kurzfristigen Ende des Marktes. Jede Verlautbarung und Aktion wird von den Märkten geprüft und hinsichtlich der zukünftigen Entwicklung der (kurzfristigen) Zinsen bewertet. Demnach ist es realistisch, anzunehmen, dass die kurzfristigen Zinsen auch die langfristigen Zinsen beeinflussen.
Neben diesen drei klassischen Zinsbestimmungsfaktoren inkludieren Bandholz et. al. [1] noch eine weitere Variable, welche die strukturelle Erhöhung der Auslandsnachfrage nach US-Staatspapieren einfangen soll.9
Bei den ökonometrischen Schätzungen in den nächsten Kapiteln greifen wir auf folgende monatlichen US-Daten zurück:10
Die zehnjährige US-Rendite (=LZINS), den dreimonatigen US-Geldmarktzins (=KZINS), als Maß für die Inflationserwartungen die Jahreswachstumsrate der Core Inflation (Headline Consumer Price Index ohne Nahrungsmittel und Energie) (=CORE), als Konjunkturmaß den ISM Index des verarbeitenden Gewerbes vom Institute for Supply Management (=ISM) und als Auslandsnachfrage (=HOLDING) auf den Quotienten von „Rest of the World Treasury Securities“ zu „Federal Government Debt Securities“.11 In Schaubild 1 sind die Variablen dargestellt.
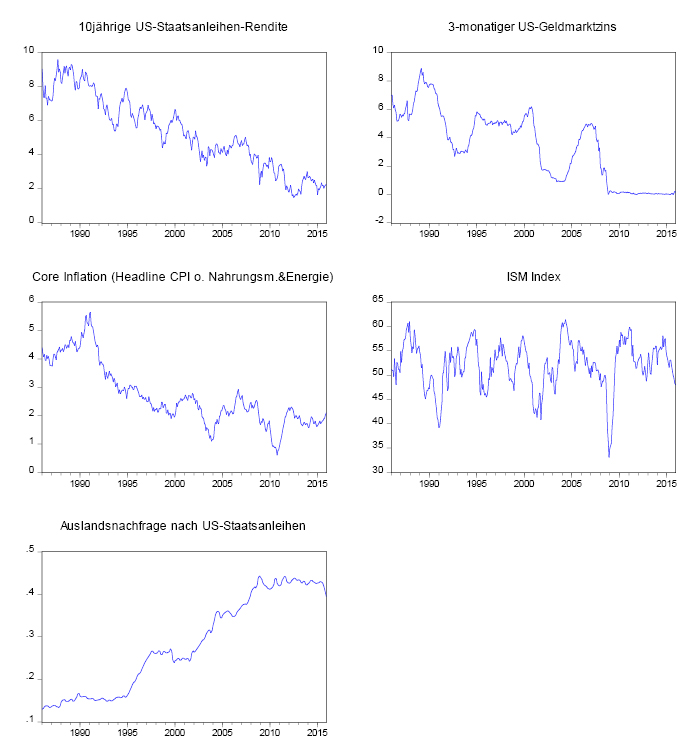
Schaubild 1: Die Variablen des BCS-Modells
3. Ökonometrische Ergebnisse
Nach einer Vielzahl von Spezifikationstests präsentierten Bandholz et. al. [1] als „Best Of“ ein Einzelgleichungsfehlerkorrekturmodell. Schätzt man dieses Modell nach (im folgenden BCS-Modell genannt), so erhält man für den gleichen, damals zugrunde gelegten Schätzzeitraum:
R² = 0.32; Adj. R² = 0.30; Standardfehler = 0.25; F-Wert= 11,98.
Abbildung 1: Schätzergebnisse für das BCS-Modell 1986.01-2005.09 (t-Werte in Klammern)
Auf den ersten Blick fällt auf, dass die Koeffizienten in Abbildung 1 nicht vollkommen identisch mit den Koeffizienten in der Originalpublikation von Bandholz et. al. [1] sind. Verantwortlich für die leichten Abweichungen dürften Datenrevisionen sein.
Verlängert man den Schätzzeitraum bis Dezember 2015 (2015.12), erhält man folgende Schätzergebnisse:
R² = 0.25; Adj. R² = 0.23; Standardfehler = 0.25; F-Wert= 12,78.
Abbildung 2: Schätzergebnisse für das BCS-Modell 1986.01-2015.12 (t-Werte in Klammern)
Folgende Dinge sind auffällig:
Der Anteil der erklärten Streuung fällt von 30% auf 25%.
Abweichungen von der langfristigen Kointegrationsbeziehung werden nun langsamer abgebaut. Der Koeffizient des Fehlerkorrekturterms sinkt von 0,26 auf 0,14.
Die langfristige Semi-Elastizität der Kerninflation ist deutlich von 0,65 auf 0,40 gesunken.
Die langfristige Reaktion des Langfristzinses auf Veränderungen der Auslandsnachfrage ist dagegen elastischer geworden (von -5,87 auf -8,37).
Führt man einen Wald-Test auf Koeffizientengleichheit insgesamt durch, muss diese Nullhypothese mit einer Irrtumswahrscheinlichkeit von nahezu 0% abgelehnt werden (siehe Abbildung 3).

Abbildung 3: Wald-Test auf Koeffizientengleichheit
Ein Blick auf die Residuen der Schätzgleichung aus Abbildung 2 erweckt allerdings nicht den Eindruck, dass sich seit der amerikanischen Finanzkrise etwas Grundlegendes geändert hat (siehe Schaubild 2). Die Ausschläge am aktuellen Rand halten sich im historischen Rahmen. Auch das Muster scheint sich nicht auffällig geändert zu haben.
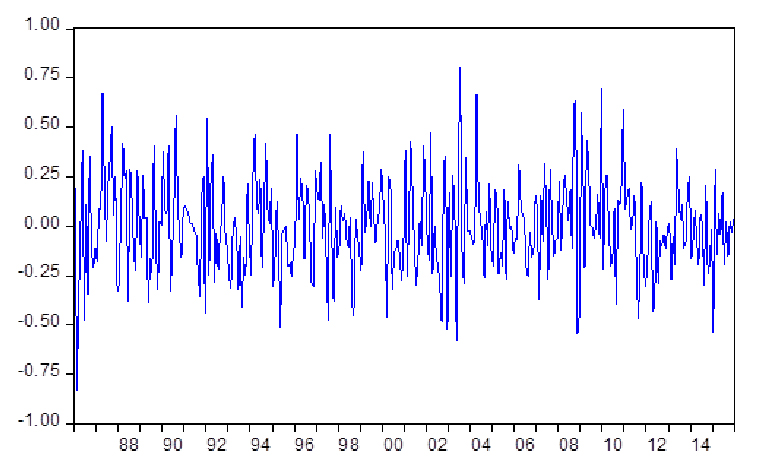
Schaubild 2: Residuen des BCS-Modells mit erweitertem Schätzzeitraum
Der Cusum-Test und der Cusum-Square-Test (Irrtumswahrscheinlichkeit < 10%) geben keine Hinweise auf Instabilitäten des Schätzansatzes. Auf der anderen Seite zeigt der Chow-Strukturbruch-Test (siehe Abbildung 4), dass die Nullhypothese keines Strukturbruchs ab Oktober 2005 (2005.10) abgelehnt werden muss.

Abbildung 4: Chow Breakpoint Test
Bandholz et. al. [1] führen in ihrem Papier auch umfangreiche Out-of-Sample-Tests durch, d. h. sie prognostizieren den US-Zins über den zugrunde liegenden Stützzeitraum hinaus. Sie generieren 120 rekursive Vorhersagen bis zu 12 Monate im Voraus, wobei sie die unabhängigen Variablen jeweils auf Basis eines für die jeweilige Variable angepassten Random-Walk-Modells prognostizieren.12 Als Prognosekriterien dienen der sogenannte Root-Mean-Squared-Error (RMSE), der die durchschnittliche Prognoseabweichung misst, und die Vorzeichentrefferquote, die angibt, wie hoch der Anteil der korrekten Richtungsvorhersage ist. Vergleicht man anhand dieser beiden Prognosegütemaße die Prognosen für den zehnjährigen US-Staatsanleihen, sieht man, dass die Vorhersagequalität des BCS-Modells auch für den bis Dezember 2015 erweiterten Stützzeitraum ähnlich gut ist (s. Abbildung 5).
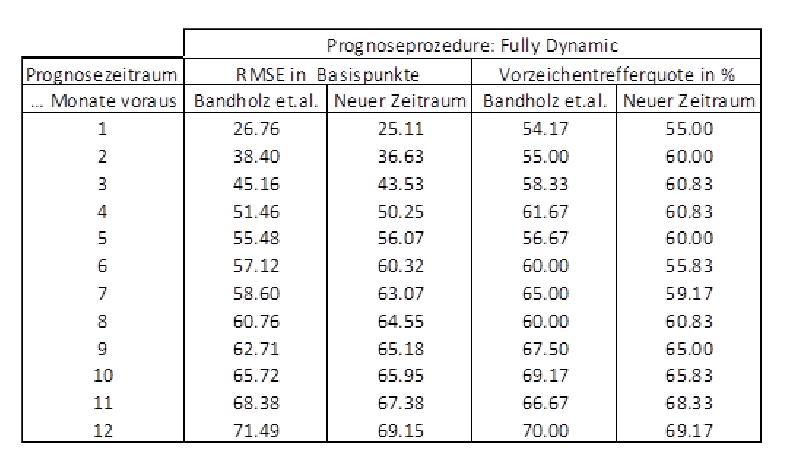
Abbildung 5: Vergleich von RMSE und Vorzeichentreffer des BCS-Modells
4. Die Erweiterung um die monetäre Basis
Wie eingangs erwähnt, verfolgt die FED seit der Finanzkrise einen sehr expansiven geldpolitischen Kurs.13 Die Notenbankzinsen wurden kräftig gesenkt, darüber hinaus griff die FED auf verschiedene Maßnahmen quantitativer Lockerungen zurück. Ziel der quantitativen Lockerung ist es, die Kapitalmarktzinsen auf breiter Front zu drücken und damit das gesamte Zinsspektrum zu beeinflussen, um letztendlich Kreditnachfrage und Güternachfrage anzukurbeln. Als Maß für die quantitative Lockerung verwenden wir die monetäre Basis. Setzt man diese Größe in Relation zum nominalen Bruttoinlandsprodukt der USA, so sieht man in Schaubild 3, dass seit dem Ausbruch der Finanzkrise 2008 dieses Verhältnis kräftig gestiegen ist.
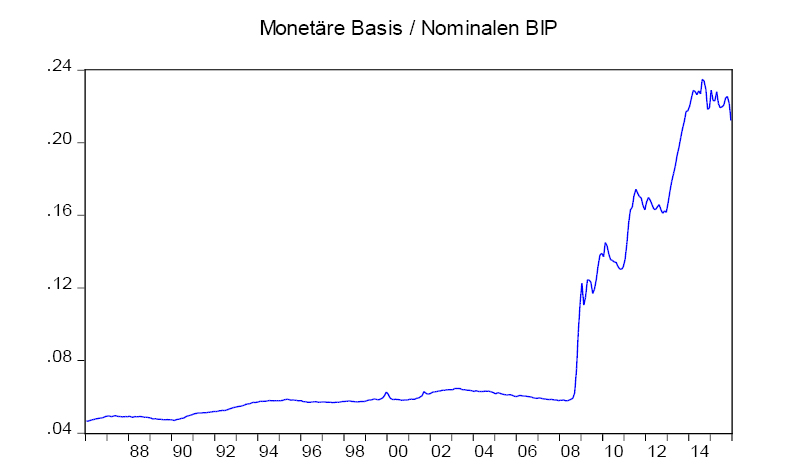
Schaubild 3: Monetäre Basis im Verhältnis zu nominalen BIP
Im nächsten Schritt versuchen wir, diese Variable in den Schätzansatz zu integrieren, um beurteilen zu können, ob und wie stark eine Ausweitung der monetären Basis auf den zehnjährigen US-Zins wirkt.14
Wir wählen dabei das von Bandholz et. al. [1] beschriebene Prozedere, d. h. wir schätzen ein Vektorfehlerkorrekturmodell (=VECM) und prüfen, ob es in einen Einzelgleichungsfehlerkorrekturansatz (=SEECM) überführbar ist.
Bis auf den ISM Index des verarbeitenden Gewerbes vom Institute for Supply Management (=ISM) sind alle Variablen - die zehnjährige Rendite von US-Staatsanleihen (=LZINS), der dreimonatige US-Geldmarktzins (=KZINS), Core Inflation (Headline CPI ohne Nahrungsmittel und Energie) (=CORE), die Auslandsnachfrage nach amerikanischen Staatspapieren (=HOLDING) und das Verhältnis zwischen der monetären Basis und dem nominalen BIP (=K_MB_GDP) – scheinbar integriert vom Grade 1 bzw. nicht stationär.15 Damit ist die Grundvoraussetzung für die Anwendung der Kointegrationsanalyse erfüllt. Im nächsten Schritt wird die Lagordnung bestimmt. Dafür wird ein unrestringiertes VAR-Modell nur mit den I(1)-Variablen geschätzt. Die Informationskriterien von Schwarz und Hannan-Quinn (siehe Abbildung 6) empfehlen eine optimale Laglänge von 2.
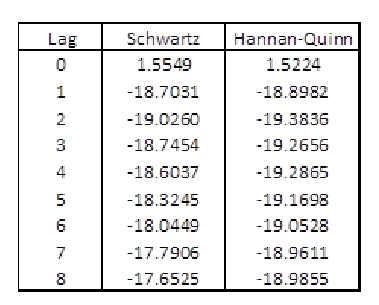
Abbildung 6: Test auf Laglänge
Die Anzahl der Kointegrationsbeziehungen zwischen den I(1)-Variablen wird mit Hilfe der Trace- und der Maximum-Eigenvalue-Statistik bestimmt. Beide Tests empfehlen eine Restriktion des Systems auf nur eine Kointegrationsbeziehung (Irrtumswahrscheinlichkeit < 1%, siehe Abbildung 7).
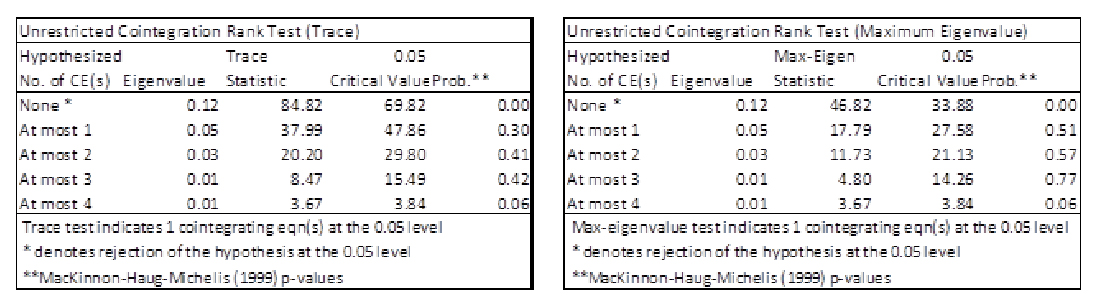
Abbildung 7: Test auf Anzahl der Kointegrationsbeziehungen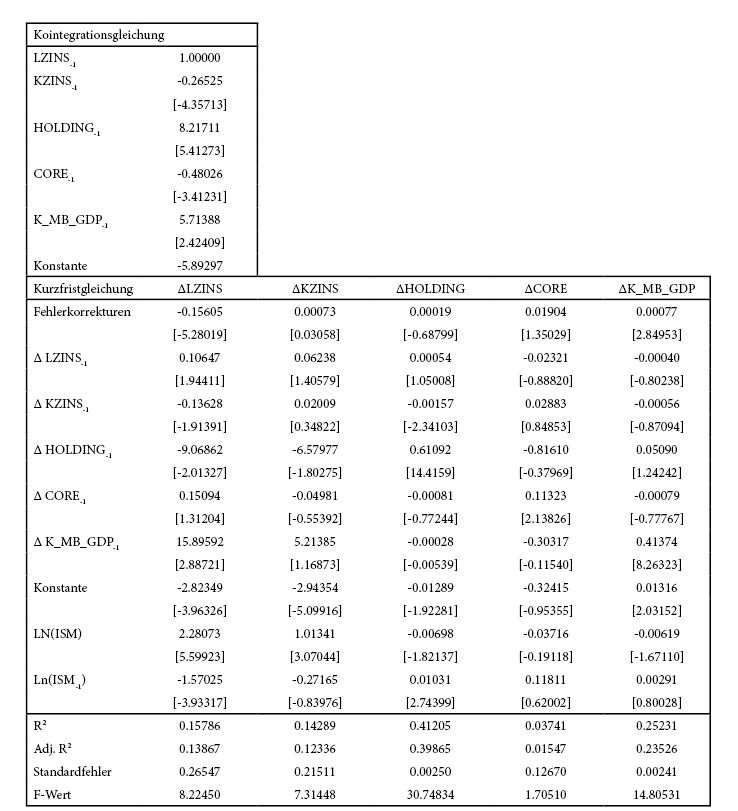
Abbildung 8: VECM (t-Werte in Klammern)
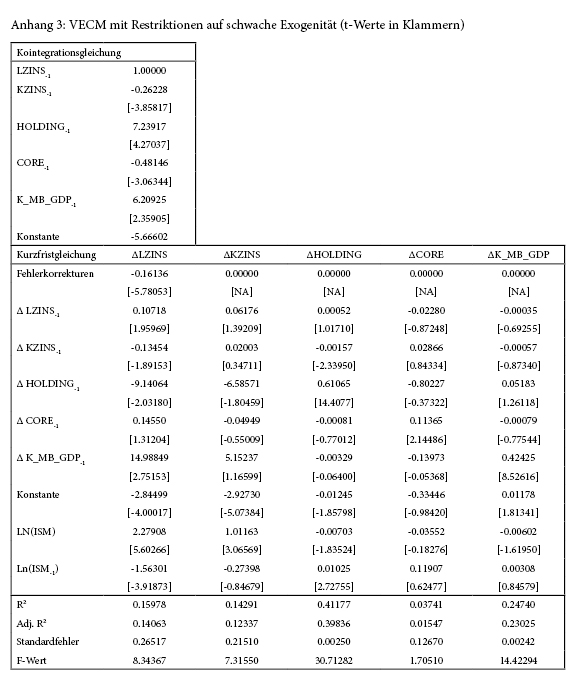
Bei der Schätzung des VECM berücksichtigen wir in Analogie zu Bandholz et. al. [1] den ISM als Konjunkturvariable (logarithmiert) kontemporär und mit der ersten Verzögerung als stationäre exogene Variable. Die Schätzergebnisse (Abbildung 8) zeigen, dass alle Langfristvariablen signifikant sind und das richtige Vorzeichen aufweisen. In diesem Zusammenhang fällt auf, dass die monetäre Basis einen negativen Effekt auf den Zins hat. Dieser Effekt wird auch durch andere Untersuchungen bestätigt.16 Der Koeffizient des Fehlerkorrekturterms der LZINS-Gleichung ist hoch signifikant negativ (siehe Abbildung 8) und deutet auf die (schwache) Endogenität der zehnjährigen US-Staatsanleiherendite hin. Restringiert man das System in der Art, das man (schwache) Exogenität aller anderen Variablen außer LZINS unterstellt, kann man diese Hypothese nur mit einer Irrtumswahrscheinlichkeit von 4,5% nicht ablehnen (Abbildung 9).17

Abbildung 9: Test auf (schwache) Exogenität im VECM
Der Befund einer schwach endogenen Staatsanleihenrendite erlaubt es, auf ein Einzelgleichung-Fehlerkorrekturmodell (=SEECM) überzugehen18, wodurch sich die Effizienz der Schätzung verbessern kann. Das SEECM entspricht der Zinsgleichung des VECM, nur dass für alle stationären Variablen der Kurzfristgleichung kontemporäre und, wie von Banerjee et. al. [12] empfohlen, u. a. bis zu drei Perioden verzögerte Werte aufgenommen werden.19 In einem nachfolgenden Auswahlprozess werden die nicht signifikanten Koeffizienten der stationären Variablen (Irrtumswahrscheinlichkeit > 1%) sukzessive auf Null gesetzt.20 Als finales Ergebnis erhalten wir Abbildung 10.
R² = 0.26; Adj. R² = 0.25; Standardfehler = 0.25; F-Wert= 13,98; LM(1) = 2,22; LM(4) = 1.09; ARCH(1) = 0.66; ARCH(4) = 1.29; JB = 5,53; CUSUM: stabil; CUSUM Square: stabil.
Abbildung 10: SEECM mit Monetärer Basis (t-Werte in Klammern)
Die Koeffizienten der Langfristbeziehung bzw. Kointegrationsbeziehung haben das erwartete Vorzeichen und sind bis auf den Koeffizienten der monetären Basis hoch signifikant. Die geschätzten Koeffizienten gleichen im Großen und Ganzen den Ergebnissen der Langfristgleichung, die sich aus dem Johansen-Verfahren [14] (siehe Abbildung 7) ableiten lassen, und den Ergebnissen bei Bandholz et. al. [1]. Dies lässt auf eine gewisse methodenunabhängige Stabilität des Zusammenhangs schließen.
Der Koeffizient des kurzfristigen Zinses in der Kointegrationsbeziehung beträgt 0,28. Ein Anstieg des Kurzfristzinses um zehn Basispunkte würde den zehnjährigen Zins um ca. drei Basispunkte ansteigen lassen. Die Zinsstrukturkurve würde in diesem Fall bzw. bei einer Zinsstraffungspolitik der Notenbank flacher (oder sogar invers) werden.
Der Koeffizient der Kerninflation als Maß für die Inflationserwartungen in der Langfristbeziehung beträgt 0,5. Ein Anstieg dieser Variable um 1% würde den zehnjährigen Zins also um 50 Basispunkte ansteigen lassen.
Die Auslandsnachfrage nach US-Staatsanleihen hat sich seit Mitte der achtziger Jahre bis zum heutigen Zeitpunkt fast vervierfacht (von 12% auf 40%). Bringt man diesen Sachverhalt mit den Schätzergebnissen in Verbindung, bedeutet dies für sich genommen allein schon ein Absinken der Rendite für zehnjährige US-Staatsanleihen um rund 190 Basispunkte [(0,4-0,12) ·-6,65=-1,86].21
Der Koeffizient des Verhältnisses von monetärer Basis und dem nominalen US-BIP beträgt -4,7. Dieser Quotient stieg zwischen 2008 und 2015 von 6% auf 22%. Dieser starke Anstieg impliziert eine langfristige Senkung der Staatsanleihenrendite um ca. 75 Basispunkte [(0,22-0,06) ·-4,7=0,75].22 Dieses Ergebnis ist mit Vorsicht zu interpretieren, da der Koeffizient mit einer Irrtumswahrscheinlichkeit von 12,3% nur schwach abgesichert ist.
Eine Erhöhung des ISM-Index erhöht den zehnjährigen Zins. Konjunkturänderungserwartungen haben allerdings nur in der sehr kurzen Frist eine hohe Bedeutung, da dieser Effekt in den darauf folgenden drei Monaten wieder schnell ausebbt. Man kann deshalb von einer Art Überschießen des Zinses auf Konjunkturerwartungen sprechen.
Der Koeffizient des Fehlerkorrekturterms ist negativ und gemessen an den kritischen Werten von Banerjee et al. [12] signifikant von null verschieden. Damit ist die Bedingung für ein langfristiges stabiles Gleichgewicht bzw. eine Kointegrationsbeziehung zwischen den I(1)-Variablen erfüllt. Die Anpassungsgeschwindigkeit der Staatsanleihenrendite an seinen fundamental bestimmten Gleichgewichtswert mit einem Parameterwert von -0,14 kann mit einer Halbwertszeit von vier bis fünf Monaten gleichgesetzt werden, d. h. dass die Staatsanleihenrendite nach einem exogenen Schock in weniger als fünf Monaten den Abstand zu seinem Gleichgewichtskurs zur Hälfte abbaut.
Bei einer Irrtumswahrscheinlichkeit von < 5% geben Breusch-Godfrey-Lagrange-Multiplikator-Tests (LM) keine Hinweise auf Autokorrelation in den Residuen (1. und 4. Ordnung), desgleichen kann der Lagrange-Multiplikator-Test auf autoregressiv bedingte Heteroskedastizität (1. und 4. Ordnung) in den Störtermen keine Verletzungen der Grundannahmen des Schätzansatzes feststellen. Ferner bestätigt der Jarque-Bera-Test die Normalverteilungsannahme für die Residuen und CUSUM-Tests geben keine Hinweise auf Parameter- oder Varianzinstabilität.
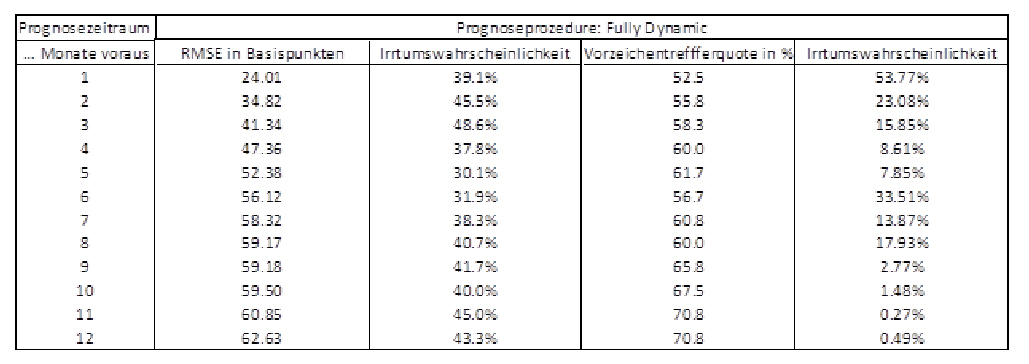
Abbildung 11: RMSE und Vorzeichentrefferquote des erweiterten SEECM
Mit diesem neuen SEECM führen wir nun auch Out-of-Sample-Tests in der schon in Kapitel 3 beschriebenen Art durch. Die Ergebnisse dazu finden sich in Abbildung 11. Vergleicht man RMSE und Vorzeichentrefferquote mit den Ergebnissen in Abbildung 5, sieht man, dass der RMSE sich meistens leicht verringert hat, während sich die Vorzeichentrefferquoten allesamt sehr ähneln. Das heißt, dass die Hinzunahme der monetären Basis als weitere Erklärungsvariable prognostisch keine großartige Verbesserung bringt. Darüber hinaus zeigen Diebold-Marino-Tests23, dass der RMSE des erweiterten SEECM nicht signifikant besser ist als ein einfacher Random Walk (ohne Drift). Allerdings ist die Vorzeichentrefferquote des erweiterten SEECM ab einem Prognosezeitraum von mehr als neun Monaten besser als ein „Münzwurf“. Ab diesem Zeitpunkt ist die Vorzeichentrefferquote signifikant größer als 50% (Irrtumswahrscheinlichkeit < 5%, auf 10%-Niveau auch für Monate 4 und 5).24 Zusammenfassend deuten die Out-of-Sample-Tests darauf hin, dass die Prognose der US-Staatsanleihenzinsen auf Basis von Makro-Variablen seit der unorthodoxen Geldpolitik der FED schwieriger geworden ist.25
5. Zusammenfassung
Seit der Finanzkrise verfolgt die FED einen sehr expansiven geldpolitischen Kurs. Die Zinsen wurden auf historische Niedrigstniveaus gesenkt, darüber hinaus griff die FED auf verschiedene Maßnahmen quantitativer Lockerungen zurück. Trotz dieser Ereignisse zeigen die ökonometrischen Analysen in diesem Papier, dass die klassischen Einflussfaktoren (Notenbankzinsen, Inflationserwartungen, Auslandsnachfrage nach US-Staatsanleihen) weiterhin gute Erklärungskraft haben. Allerdings sind diese Zusammenhänge in jüngster Zeit nicht mehr so stabil. Darüber hinaus kann man feststellen, dass das Anleiheaufkaufprogramm der amerikanischen Notenbank wohl einen messbaren Einfluss auf den zehnjährigen US-Staatsanleihenzins hat.
Die Aufgabe der zukünftigen Forschung ist es, zu prüfen, ob es sich um vorübergehende Instabilitäten handelt oder nach dem Ende der expansiven unorthodoxen Geldpolitik der FED die ursprünglichen, sehr stabilen fundamentalen Zusammenhänge zwischen Zinsen und seinen Fundamentalfaktoren wieder gültig sind.
Ob QE ein wirkungsvolles geldpolitisches Instrumentarium ist, kann nicht letztendlich und generell beantwortet werden. Im Ansatz wurde nur untersucht, ob die FED-Politik auf die Zinsen wirkt. Die Antwort hierfür kann wohl bejaht werden. Ob die FED damit allerdings die Kreditnachfrage, die Güternachfrage und die Konjunktur stimulieren konnte, bleibt ebenfalls weiterer Forschung vorbehalten.
6. Disclaimer
Alle Meinungsaussagen oder Einschätzungen in diesem Dokument geben die Einschätzung des Verfassers bzw. der Verfasser wieder. Die hierin zum Ausdruck gebrachten Meinungen spiegeln nicht zwangsläufig die Meinungen der UniCredit Bank AG wider. Verantwortlich für den Inhalt ist allein der jeweilige Autor.
7. Abkürzungen
BCS-Modell:
Zinsmodell von Bandholz et. al. (2009)
BIZ:
Bank für Internationalen Zahlungsausgleich
CORE:
US Core Inflation (Headline Consumer Price Index ohne Nahrungsmittel und Energie)
EZB:
Europäische Zentralbank
FED:
Federal Reserve System (US-Notenbank)
HOLDING:
Anteil der vom Ausland gehaltenen US-Staatsanleihen gebildet aus dem Verhältnis von „Rest of the World Treasury Securities“ und „Federal Government Debt Securities“
ISM:
Index des Verarbeitenden Gewerbes vom Institute for Supply Management
IWF:
Internationaler Währungsfonds
K_MB_GDP:
Das Verhältnis zwischen der monetären Basis der FED und dem nominalen US-BIP
KZINS:
US-Geldmarktzins für Dreimonatsgeld
LZINS:
Zins für zehnjährige US-Staatsanleihen
OECD:
Organization of Economic Cooperation and Development
QE:
Quantitative Easing
RMSE:
Root Mean Squared Error
SEECM: Einzelgleichungsfehlerkorrekturmodell
VECM:
Vektorfehlerkorrekturmodell
8. Literatur
[1] Bandholz, Harm; Clostermann, Jörg; Seitz, Franz (2009): “Explaining the US Bond Yield Conundrum”. In: Applied Financial Economics 19 (7), S. 539–550.
[2] Belke, Ansgar; Gros, Daniel; Osowski, Thomas (2016): “Did Quantitative Easing Affect Interest Rates Outside the US? – New Evidence Based on Interest Rate Differentials. Federal Reserve Bank of San Francisco (FRBSF Economic Letters 2016-20). [Online verfügbar]. https://www.ceps.eu/system/files/WD416%20Did%20QE%20affect%20interest%20rates_0.pdf. (zuletzt geprüft am 29.09.2016).
[3] Fawley, Brett W.; Neely, Christopher J. (2013): “Four Stories of Quantitative Easing.” In: Federal Reserve Bank of St. Louis Review 95 (1), S. 51–88.
[4] Greenspan, A. (2005): Testimony of Chairman Alan Greenspan. Federal Reserve Board‘s semiannual Monetary Policy Report to the Congress. Before the Committee on Banking, Housing, and Urban Affairs of the U.S. Senate. Washington, DC, 16.02.2005.
[5] Bernanke, Ben S. (March 20th 2006): Remarks by Ben S. Bernanke (Chairman of the Board of Governors of the Federal Reserve System) before the Economic Club of New York. New York, NY, 20.03.2006.
[6] Obstfeld, Maurice; Tesar, Linda (2015): The Decline in Long-Term Interest Rates, the WHITE HOUSE President Barack Obama. The White House/President Barack Obama. July 14, 2015 at 5:35 PM ET. [Online verfügbar]. https://www.whitehouse.gov/blog/2015/07/14/decline-long-term-interest-rates. (zuletzt geprüft am 18.08.2016).
[7] The Executive Office of the President of the United States (2015): Long Term Interest-Rate: A Survey. Council of Economic Advisors. [Online verfügbar]. https://www.whitehouse.gov/sites/default/files/docs/interest_rate_report_final.pdf,. (zuletzt geprüft am 18.08.2016).
[8] Auer, Benjamin; Rottmann, Horst (2015): Statistik und Ökonometrie für Wirtschaftswissenschaftler. Eine anwendungsorientierte Einführung. 3., überarb. u. aktualisierte Aufl. 2015. Wiesbaden: Springer Gabler (SpringerLink : Bücher).
[9] Issing, Otmar (2011): Einführung in die Geldtheorie. 15., wesentlich überarbeitete Auflage. München: Vahlen (Vahlens Kurzlehrbücher).
[10] Board of Governors of the Federal Reserve System (2016): Z.1 Financial Accounts of the United States. Flow of Funds, Balance Sheets, and Integrated Macroeconomic Accounts. Second Quarter 2016. [Online verfügbar]. https://www.federalreserve.gov/releases/z1/current/z1.pdf. (zuletzt geprüft am 18.08.2016.
[11] Wu, Tao (2014): Unconventional Monetary Policy and Long-Term Interest Rates. IMF Working Paper WP/14/189. International Monetary Fund/Institute for Capacity Development. [Online verfügbar]. https://www.imf.org/external/pubs/ft/wp/2014/wp14189.pdf. (zuletzt geprüft am 18.08.2016).
[12] Banerjee, Anindya; Dolado, Juan; Mestre, Ricardo (1998): “Error-Correction Mechanism Tests for Cointegration in a Single-Equation Framework.” In: Journal of Time Series Analysis 19 (3), S. 267–283.
[13] Engle, Robert F.; Hendry, David F.; Richard, Jean-François (1983): “Exogeneity.” In: Econometrica (Hg.: The Econometric Society) 51 (2), S. 277–304.
[14] Johansen, Søren (1992): “Cointegration in Partial Systems and the Efficiency of Single-Equation Analysis.” In: Journal of Econometrics 52 (3), S. 389–402.
[15] Derksen, Shelley; Keselmann, H. J. (1992): “Backward, Forward and Stepwise Automated Subset Selection Algorithms: Frequency of Obtaining Authentic and Noise Variables.” In: British Journal of Mathematical and Statistical Psychology 45 (2), S. 265–282.
[16] Beltran, Daniel O.; Kretchmer, Maxwell; Marquez, Jaime; Thomas, Charles P. (2013): “Foreign Holdings of U.S. Treasuries and U.S. Treasury Yields.” In: Journal of International Money and Finance 32 (February), S. 1120–1143.
[17] Kaminska, Iryna; Zinna, Gabriele (2014): Official Demand for U.S. Debt: Implications for U.S. Real Interest Rates. IMF Working Paper WP/14/66. International Monetary Fund. [Online verfügbar]. https://www.imf.org/external/pubs/ft/wp/2014/wp1466.pdf. (zuletzt geprüft am 18.08.2016).
[18] Carvalho, Daniel; Fidora, Michael (2015): Capital Inflows and Euro Area Long-Term Interest Rates. June 2015. European Central Bank (ECB Working Paper 1798).[Online verfügbar]. http://www.ecb.europa.eu/pub/pdf/scpwps/ecbwp1798.en.pdf. (zuletzt geprüft am 29.09.2016).
[19] Diebold, Francis X.; Mariano, Roberto S. (1995): “Comparing Predictive Accuracy.” In: Journal of Business & Economic Statistics 13, S. 253–263.
[20] Cheung, Yin-Wong; Chinn, Menzie D.; Pascual, Antonio Garcia (2005): “Empirical Exchange Rate Models of the Nineties: Are Any Fit to Survive?” In: Journal of International Money and Finance 24, S. 1150–1175.
[21] Bauer, Michael D.; Hamilton, James D. (2015): Robust Bond Risk Premia. Federal Reserve Bank of San Francisco (Working Paper Series, Working Paper 2015-15). [Online verfügbar]. http://www.frbsf.org/economic-research/files/wp2015-15.pdf. (zuletzt geprüft am 18.08.2016).
[22] Bauer, Michael D.; Hamilton, James D. (2016): Do Macro Variables Help Forecast Interest Rates? Federal Reserve Bank of San Francisco (FRBSF Economic Letter 2016-20). [Online verfügbar]. http://www.frbsf.org/economic-research/publications/economic-letter/2016/june/do-macroeconomic-variables-help-forecast-interest-rates/. (zuletzt geprüft am 29.09.2016)
1 Eine ausführliche Beschreibung dieser geldpolitischen Maßnahmen findet sich bei Belke et. al. [2] und Fawley/Neely [3].
2 Greenspan, 2005 [4].
3 Bernanke, 2006 [5]. Eine intensive Analyse für das seit 30 Jahren zu beobachtenden Absinken der langfristigen US-Zinsen findet sich in Obstfeld/Tesar [6] und The Executive Office of the President of the United States [7].
4 Auer/Rottmann, 2015 (S. 587 ff.) [8].
5 Issing, 2011 (S. 258) [9]
6 Issing, 2011 (S. 188 ff.) [9].7 Issing, 2011 (S. 123 ff.) [9].
8 Issing, 2011 (S. 123-124) [9].
9 Bandholz et. al. [1] vermuten, dass die Erhöhung von Devisenreserven einiger asiatischer Länder, das Recycling der Petro-Dollar,
das veränderte Anlageverhalten von institutionellen Investoren und die weltweite Erhöhung der Liquidität die Risikoprämie für US-amerikanische Staatspapiere und infolgedessen auch das Zinsniveau reduziert hat.
10 Die Daten können von den Autoren angefordert werden.
11 Board of Governors of the Federal Reserve System [10], L132, Zeile 10 und L106 Zeile 20, jeweils von Quartalszahlen in Monatsdaten umgerechnet.
12 Bandholz et al., S. 547 ff. [1].
13 Dieser wurde durch die sukzessive Rückführung der Wertpapierkäufe seit Oktober 2014 und die im Dezember 2015 erfolgte geringfügige Zinserhöhung um 0,25 Prozentpunkte im Zeitablauf abgeschwächt.
14 Die Stärke des Einflusses der monetären Basis auf den zehnjährigen US-Zins hängt auch von der Laufzeitenstruktur der Staatspapiere ab, welche die FED aufgekauft hat. Allerdings sind hierüber keine öffentlichen Daten verfügbar.
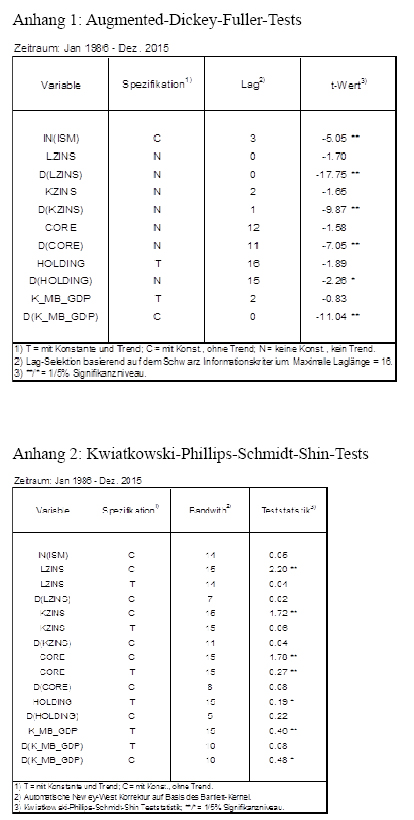
15 Im Anhang 1 und 2 finden sich die dazugehörigen Unit-Root- bzw. Stationaritätstests.
16 Wu, 2014 [11]. Wu zeigt darüber hinaus, dass das Anleihenaufkaufprogramm der FED über mehrere Kanäle die Staatsanleiherenditen beeinflusst.
17 Im Anhang 3 befinden sich die Ergebnisse des VECM mit den inkludierten Restriktionen auf schwache Exogenität.
18 Engle et. al., 1983 [13]; Johansen, 1992 [14].
19 Banerjee et al. [12] (S. 275) empfehlen, das SEECM auch durch Leads der stationären Variablen anzureichern, um
Stichprobenfehler in zu kleinen Stichproben zu reduzieren. Wir verzichten auf dieses Vorgehen, zum einen, weil die Stichprobe mit n=360 relativ groß ist, zum anderen, weil wir später mit diesem Ansatz Out-of-Sample-Prognosen generieren möchten und uns dies nötigen würde, Lead-Variablen zu prognostizieren.
20 Derksen/Keselman [15].
21 Beltran et. al. [16] stellen in ihrer Untersuchung auch einen signifikanten Effekt der Auslandsnachfrage auf die US-Staatsanleiherenditen fest (siehe auch Kaminska/Zinna [17]).
Dieser Effekt scheint auch für das Euroland zu gelten, siehe Carvalho/Fidora [18].
22 Kaminska/Zinna [17] kommen in ihrer Analyse zu einer ähnlichen Größenordnung, allerdings stellen sie bei ihrer Schätzung auf die Realrendite ab.
23 Zur Berechnung der Irrtumswahrscheinlichkeit des RMSE siehe Diebold/Mariano [19].
24 Zur Berechnung der Irrtumswahrscheinlichkeit der Vorzeichentrefferquote siehe Cheung et. al. [20].
25 Bauer/Hamilton [21, 22] stellen grundsätzlich in Frage, ob eine Prognose von Zinsen auf Basis von Makro-Variablen überhaupt möglich ist.
Anhang

Dr. Harm Bandholz
Dr. Harm Bandholz ist US-Chefvolkswirt der UniCredit Bank in New York. In seiner Tätigkeit analysiert er sowohl konjunkturelle Entwicklungen als auch geld- und fiskalpolitische Tendenzen, insbesondere solche mit Relevanz für die Finanzmärkte. Vor seinem Wechsel zur UniCredit arbeitete Herr Bandholz als wissenschaftlicher Mitarbeiter am Ifo-Institut in München sowie am Lehrstuhl für angewandte Makroökonomie der Universität Hamburg. Er ist Mitglied des Economic Club of New York, des Forecasters Club of New York, des American Council on Germany, der New York Society of Security Analysts und des CFA Institute.
Harm Bandholz is the Chief US Economist for UniCredit. In his role, he analyzes the macroeconomy as well as monetary and fiscal policy developments, in particular those with relevance for financial markets. Before joining the bank, Dr. Bandholz worked as a Research Assistant in the Department of Business Cycle Analyses & Financial Markets of the Ifo Institute for Economic Research in Munich, and as a Teaching and Research Assistant at the Department of Economics at Hamburg University. He is a member of the Economic Club of New York, the Forecasters Club of New York, the American Council on Germany, the New York Society of Security Analysts, and the CFA Institute.
Kontakt / Contact:

Prof. Dr. Jörg Clostermann
Prof. Dr. Jörg Clostermann lehrt Volkwirtschaftslehre und Quantitative Methoden an der Technischen Hochschule Ingolstadt. Vor seiner Berufung arbeitete er in der Hauptabteilung Volkwirtschaft der Deutschen Bundesbank in Frankfurt, Abteilung Außenwirtschaft. Prof. Clostermann berät seit vielen Jahren Banken und Unternehmen auf dem Gebiet Indikatoren und Prognosen. Er ist darüber hinaus Mitglied des Aktionskreises Stabiles Geld.
Professor Joerg Clostermann teaches Economics and Statistics at Ingolstadt Technical University of Applied Sciences. Before his professorship, he worked at the Deutsche Bundesbank in the division Economics and the department International Economics. For many years now, Professor Clostermann has been acting as a consultant for banks and enterprises in the area of economic indicators and economic forecasts. Furthermore, he is a member of the Aktionskreis: Stabiles Geld.
Kontakt / Contact:

Prof. Dr. Franz Seitz
Prof. Dr. Franz Seitz lehrt Volkswirtschaftslehre, insbesondere Geldpolitik und Finanzmärkte, an der Ostbayerischen Technischen Hochschule in Weiden. Zugleich ist er federführendes Mitglied im Aktionskreis Stabiles Geld. Vor seiner Berufung als Professor arbeitete er in der Hauptabteilung Volkswirtschaft der Deutschen Bundesbank, Abteilung Geld, Kredit und Kapitalmarkt, in Frankfurt am Main. Prof. Seitz ist Autor zahlreicher Artikel in nationalen und internationalen Fachzeitschriften. Seit etlichen Jahren fungiert Prof. Seitz in mehreren Projekten als Berater der Europäischen Zentralbank und der Deutschen Bundesbank.
Professor Franz Seitz teaches Economics with a special focus on Monetary Policy and Financial Markets at Weiden Technical University of Applied Sciences. He is also one of the leading members of the Aktionskreis Stabiles Geld. Before his professorship, he worked at the Deutsche Bundesbank in the division Money, Credit and Capital Markets. Professor Seitz is author of numerous articles in national and international journals. For many years now, Professor Seitz has been acting as a consultant in different projects for the Deutsche Bundesbank and the European Central Bank.
Kontakt / Contact:
