Drive system for optimized traction on tracked mobile robots
DOI Nr.: https://doi.org/10.25929/w2tf-ks21
Ludwig Barthuber
Technische Hochschule Deggendorf
Technologie Campus Cham
Peter Firsching
Technische Hochschule Deggendorf
Technologie Campus Cham
ABSTRACT
Räder und Gleisketten stellen in der heutigen bodengebundenen, mobilen Robotik den Standard bei den Antriebselementen dar. Dabei ist die optimale Verbindung zwischen Fahrzeug und Umwelt essentiell. Hinsichtlich Lokalisations-mechanismen, der Optimierung des Vortriebs und der Beurteilung der Umgebung gibt es mechanische und steuerungstechnische Ansätze, die diese Schnittstelle in Bezug auf Kraftübertragung und mathematischer Beschreibung verbessern. Jedoch gibt es derzeit keine Ansätze, um die Traktion in unwegsamem Gelände durch zusätzlichen Krafteinsatz zu verbessern. Daher wird hier ein Konzept eines Gleiskettenantriebes vorgeschlagen, mit dem gezielt auf den Kontaktpunkt des Antriebselements und des Untergrundes Einfluss genommen werden kann. Es kann gezeigt werden, dass der Antrieb auf verschiedene Untergründe optimierbar ist. Zudem wird die Adaption und Integration in bestehende Roboterplattformen erörtert. Der Bedarf von drehzahl- und stromgeregelten Antrieben wird ebenfalls dargelegt und eine dem Konzept entsprechende Regelung entworfen. Das Ergebnis zeigt also einen Antrieb, der unter Vorgabe von Geschwindigkeit und Kraft eine optimale Kraftübertragung zu erreichen vermag und damit Vortrieb und Möglichkeit zur Schnittstellenbeschreibung optimiert. Mit diesem System werden mobile Roboter ertüchtigt, sich an verschiedene Oberflächen anzupassen und so speziell in natürlichen Umgebungen Gegebenheiten auszunutzen, die für reguläre Konzepte vielmehr Hindernisse darstellen. Dadurch kann eine bessere Integration des künstlich geschaffenen Systems Roboter in das natürliche Umfeld realisiert werden.
Wheels and tracks are standard drive components in today’s ground linked mobile robotics. In this regard, the optimal connection between vehicle and environment is essential. In consideration to localization mechanisms, optimization of propulsion and estimation of surface, there are mechanical and control approaches to improve this interface in terms of force transmission and mathematical description. However, currently no approaches exist for improving traction in rough terrain through additional force. Therefore we propose a novel concept of a track drive, which enables a precise interaction at the contact point between drive part and environment. It can be shown that the system may be optimized for different surfaces. Moreover, the adaption and integration in existing robot platforms is discussed. The demand of a revolution speed and current controlled drive is explained as well. Based on this concept, a suitable control is designed. The result reveals a crawler chassis that can, controlled by setting the parameters for speed and force, achieve an optimal force transmission and therefore improve propulsion and quality of mathematical interface description. With this system, mobile robots obtain the ability to adapt to different surfaces and in particular to take advantage of the special conditions given in a natural environment that are rather obstructive for common robot platforms. Thus, a better integration of the artificial system robot in natural surroundings can be realized.
KEYWORDS
Antrieb, Traktion, mobil, Roboter, Kette
1. Einleitung
Um die naturgemäß inhomogenen Einsatzgebiete für mobile Roboter zu erreichen, wurde in der Vergangenheit eine große Zahl an Lokomotionsmechanismen und damit verbunden mechanischen Konstrukten entwickelt und untersucht. Bei bodengebunden Robotern konnte sich dabei der Rad- und der Gleiskettenantrieb als Standard etablieren, wobei sich als Differentialantrieb die Kinematik im Wesentlichen durch die Kontaktfläche unterscheidet.
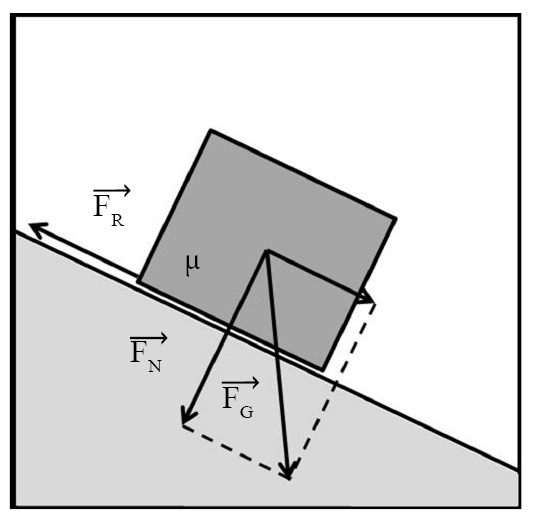
Abbildung 1: Reibungsgesetz
Vereinfacht kann die Schnittstelle zwischen Roboter und Umwelt mit Abbildung 1 dargestellt werden. Die Reibkraft FR, die der maximalen übertragbaren Antriebskraft entspricht, kann aus der Normalkraft FN und dem Reibkoeffizienten µ bestimmt werden. Die Normalkraft selbst ist von der Gewichtskraft des Roboters abhängig. Da prinzipiell leichte Systeme aus Gründen der Dynamik und Reichweite angestrebt werden, kann diese Größe nicht für Optimierungen herangezogen werden. Daher zielen vorgeschlagene Verbesserungen im Wesentlichen auf die Schnittstelle selbst ab.
In Bezug auf reelle bodengebundene Roboter wurden dazu verschiedene Ansätze vorgeschlagen. Einerseits können mechanische Eigenschaften als Indiz herangezogen werden, welche den Kontakt verbessern sollen. Vereinfacht kann dies mit einer Erhöhung von µ ausgedrückt werden. Verschiedene Arbeiten zielen darauf, die Anzahl oder die Fläche der Schnittstelle zwischen Roboter und Umgebung zu erhöhen. Hierbei sind besonders Roboter mit zwei, vier oder sechs Ketten [1-3] zu nennen. Ebenso wird mit der Adaptionsfähigkeit des Antriebssystems eine Möglichkeit zur Optimierung geschaffen. Hierbei ist eine Nachführung der Ketten zur optimalen Umschlingung von Kanten [4] möglich, ebenso wie die Anpassung der Geometrie in Höhe und Winkel der Fahrzeugfront [5].
Zu den mechanischen Optimierungen kommen mehr und mehr steuerungstechnische Ansätze, die ohne konstruktive Veränderungen Verbesserungen in der Regelung der Antriebe oder in den Aussagen über die Schnittstelle zulassen. In der Arbeit von Ojeda, Cruz, Reina & Borenstein [6] wird ein Verfahren beschrieben, bei dem über die Messung des Motorstroms Schlupf an den Rädern erkannt werden kann und so die Positionsbestimmung mittels Odometrie verbessert wird. Im Artikel von Brooks & Iagnemma [7] wird ein Verfahren vorgestellt, bei dem sowohl optisch als auch durch Vibrationsmessung unter Einbeziehung eines Bodenmodells Verbesserungen der Schnittstellenbeschreibung erreicht werden sollen. Über die sensorische Rückmeldung bei speziellen Fahrmanövern [8, 9] sollen ebenfalls Aussagen über die Bodenbeschaffenheit getroffen werden, die eine Beschreibung des
Kontaktpunktes bzw. der Kontaktfläche zulassen oder verbessern. Nachteilig ist bei
den letztgenannten, die Steuerungstechnik
betreffenden Arbeiten gemeinhin, dass die Traktion lediglich beschrieben, selbst jedoch nicht verbessert werden kann, da sie im Allgemeinen von Parametern wie dem Eigengewicht des Roboters, den Antriebselementen und den Umgebungsparametern abhängt.
Dieser Punkt wird durch Serviceroboter mit aktiver Traktionserhöhung - bspw. Fensterreinigungsroboter mit Vakuumfixierung - wesentlich verbessert. Das Verfahren bedarf jedoch erheblichen technischen Aufwandes und kann in rauer Umgebung wegen der schwierigen Abdichtung nicht eingesetzt werden. Ein weiteres Verfahren wird im Beitrag von Parness [10] vorgeschlagen. Es sollen sich sogenannte Mikrostacheln an steinigen, porösen Oberflächen verhaken. Ebenfalls setzt aber dieses Vorgehen einen gleichförmigen Untergrund voraus und kann nicht auf zum Beispiel laubbedecktem Erdboden eingesetzt werden.
Daher wird ein Kettenantrieb vorgeschlagen, der es ermöglicht, eine kontinuierliche Greifbewegung auszuführen. Als Bauform wird ein Differentialantrieb mit zwei Gleiskettenpaaren gewählt. Die Kettenpaare sind mit jeweils zwei Antrieben ausgestattet, die eine komplett unabhängige Bewegung, beziehungsweise Steuerung erlauben. Alle Ketten sind parallel angeordnet. Somit ist es möglich, während der Vortriebsbewegung eine Scherkraft in die Oberfläche einzubringen und damit die maximale Vortriebskraft, welche normalerweise durch die Gewichtskraft beschränkt ist, zu erhöhen.
2. Vorüberlegungen
Fahrzeuge aller Art bedürfen allgemein eines Kontaktelements zu ihrer Umgebung. Damit wird eine meist reibschlüssige Verbindung realisiert, die Kräfte übertragen soll. Durch die Plastizität von Oberflächen wurden vor allem für schwere Fahrzeuge Elemente eingeführt, die den Bodendruck senken sollen. Diese Elemente sind heutzutage beispielsweise als Gleisketten zu finden. Allerdings wird in der mobilen Robotik ein anderer Vorteil des Kettenantriebs ausgenutzt als bei der klassischen Verwendung wie beispielsweise an einer Schubraupe. Während die Schubraupe mit hohem Gewicht auf verformbaren Boden drückt, wird versucht, mit der Kette die Auflast zu verteilen und damit ein Einsinken zu verhindern. Dagegen erzeugt ein mobiler Roboter mit einem Gewicht von meist unter 100 kg von Natur aus einen wesentlich niedrigeren Bodendruck. Es ist allerdings so, dass mobile Roboter sich in eine unklare Umgebung einfinden müssen und daher feste Oberflächen, die für eine Fortbewegung geeignet sind, an verschiedenen, sich verändernden Positionen gegenüber dem Fahrzeug sind. Um diese möglichen Positionen möglichst gut zu erfassen, eignen sich Kettenantriebe besonders gut, da sie große Flächen abdecken im Vergleich zu punktuellen Elementen wie Rädern. Abbildung 2 soll diesen Sachverhalt schematisch darstellen, wobei die Pfeile auf Kontaktpunkte hinweisen.
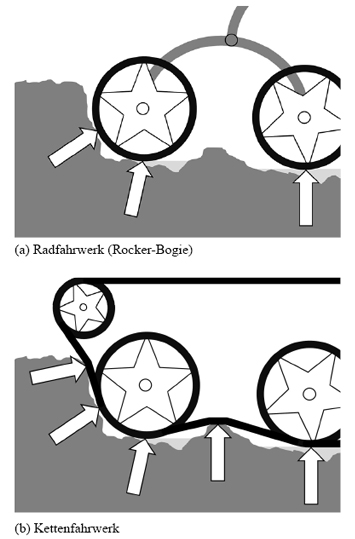
Abbildung 2: Fahrwerksarten
Werden zunächst nur Reibkräfte betrachtet, so kann festgestellt werden, dass diese von der Materialpaarung sowie der Erscheinungsform der Materialien abhängt. Dies zeigt sich beispielsweise bei festem Stein und losem Sand. Dieses Verhalten wird durch das Mohr-Coulomb-Modell physikalisch und beispielsweise durch das Bekker-Modell anwendungsbezogen beschrieben [11]. Dabei kann jeweils ein Kontaktpunkt in Abhängigkeit von innerer Reibung und Kohäsion modelliert werden. Für das Gesamtsystem ist eine Aufrechnung aller Kontaktpunkte nach den jeweiligen Gegebenheiten notwendig.
Werden zudem Verhakungen an festen Objekten berücksichtigt, so ist die reibschlüssige Verbindung während der formschlüssigen Verbindung obsolet und die gesamte Antriebskraft kann bis zum Versagen von Stegen oder Stollen von Kette oder Rad an die Umgebung übertragen werden. Schlupf tritt in diesem Fall nicht mehr auf. Eine mathematische Beschreibung von Verhakungen ist aufgrund des zufälligen Charakters mit beschriebenen Modellen nicht möglich.
Wird ein Objekt an einem festen Abhang hinsichtlich der wirkenden Kräfte untersucht, (vgl. Abbildung 1) so kann festgestellt werden, dass mit größerem Gefälle die Normalkraft zwischen den Oberflächen absinkt, die zur Beibehaltung der Position notwendige Haftreibungskraft zunimmt. Daher ist der Steigwinkel als Maß für die Bestimmung des Roboter-Untergrund-Kontakts repräsentativ. Des Weiteren ist ersichtlich, dass die maßgebende Größe Eigengewicht, welche für den horizontalen Fall direkt als Normalkraft wirkt, bei Steigungen vom Reibkontakt teilweise aufgenommen werden muss und daher dem maximal erreichbaren Vortrieb entgegensteht.
3. Gleiskettenfahrwerk
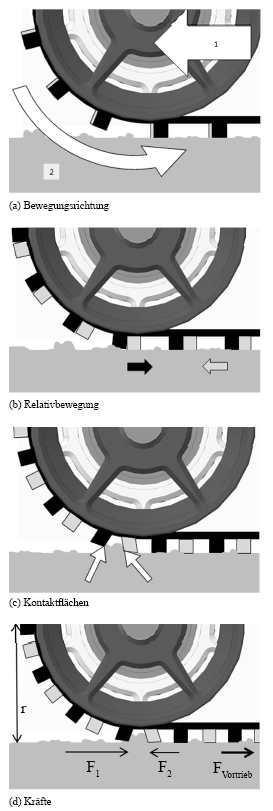
Abbildung 3: Kettenmechanik
Wie in Abbildung 3a dargestellt, entspricht der Fortbewegungsmechanismus wesentlich
dem herkömmlichen Prozess bei Gleiskettenantrieben. Die Fortbewegung (Pfeil 1) wird durch den Antrieb des Kettenrades (Pfeil 2) ermöglicht. Die Ketten werden kontinuierlich auf den Untergrund gelegt und die Räder des Roboters rollen darauf ab. Durch eine weitere parallel angeordnete Kette, die unabhängig von der ersten Kette angetrieben werden kann, ist es nun möglich, die Stege relativ zueinander zu verschieben (Abbildung 3b). Wird nun ein steifes, festes Objekt der Umgebung, wie beispielsweise eine Kante oder ein Ast, erfasst, so kann sich der Antrieb daran verklemmen (Abbildung 3c). Die an die Umwelt übertragbare Kraft hängt dann nicht nur mehr vom Eigengewicht des Roboters ab, sondern zudem von der aufgebrachten Greifkraft des Antriebes. Zum Erreichen der Kraftwirkung auf den Untergrund ist die Kraftübertragung vom Antriebsrad auf die Gleiskette wesentlich. Daher muss entweder ein ausreichender Reibschluss oder eine formschlüssige Verbindung vorgesehen werden. Es ist daher zwischen der klassischen Herkunft der Gleisketten zu unterscheiden, bei dem die Kette lose auf den Rollen und Rädern liegt und heutigen, häufig anzutreffenden Anwendungen, bei denen bereits eine formschlüssige Verbindung erreicht wird.
Es ist ersichtlich, dass eine Antriebskette nicht zum Vortrieb beiträgt, sondern lediglich zur Erhöhung der Traktion dient. In Abbildung 3d sind Kräfte aufgetragen, die diese Wirkungsweise veranschaulichen sollen. Die Größe F1 beschreibt dabei die Kraft, die zur Fortbewegung notwendig ist. Kraft F2 ist dem entgegengerichtet und betragsmäßig kleiner, so dass gilt:
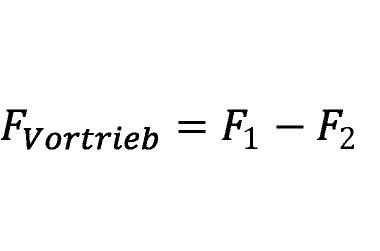
Dabei beschreibt Fges die nach außen wirkende Vortriebkraft. Auf vektorielle Schreibweise kann in der zweidimensionalen Darstellung verzichtet werden, da die Kräfte konstruktiv nur parallel auftreten können und so entsprechend direkt entgegengesetzt gerichtet sind.
Mit dem Radius r können die Antriebsmomente mit M1=F1∙r und M2=F2∙r berechnet werden. Die Vortriebskraft ergibt sich dann aus den Motormomenten aus
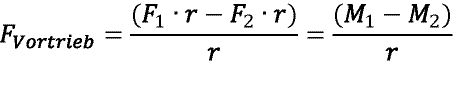
Aus der Formel für die Leistung der Drehbewegung P=Mω und den beiden entgegen gerichteten Momente M1 und M2 ergibt sich die Gesamtleistung der Antriebe, die zur Verfügung gestellt werden muss
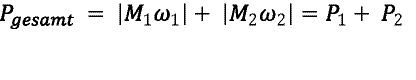
Durch Umformung der Gleichung 3.1 erschließt sich, dass F1 aus den Komponenten der Vortriebskraft FVortrieb und der Reaktionskraft zu F2 besteht.

Durch Variation von F2 ist es also möglich, die für den Vortrieb eingesetzte Energie zu optimieren.
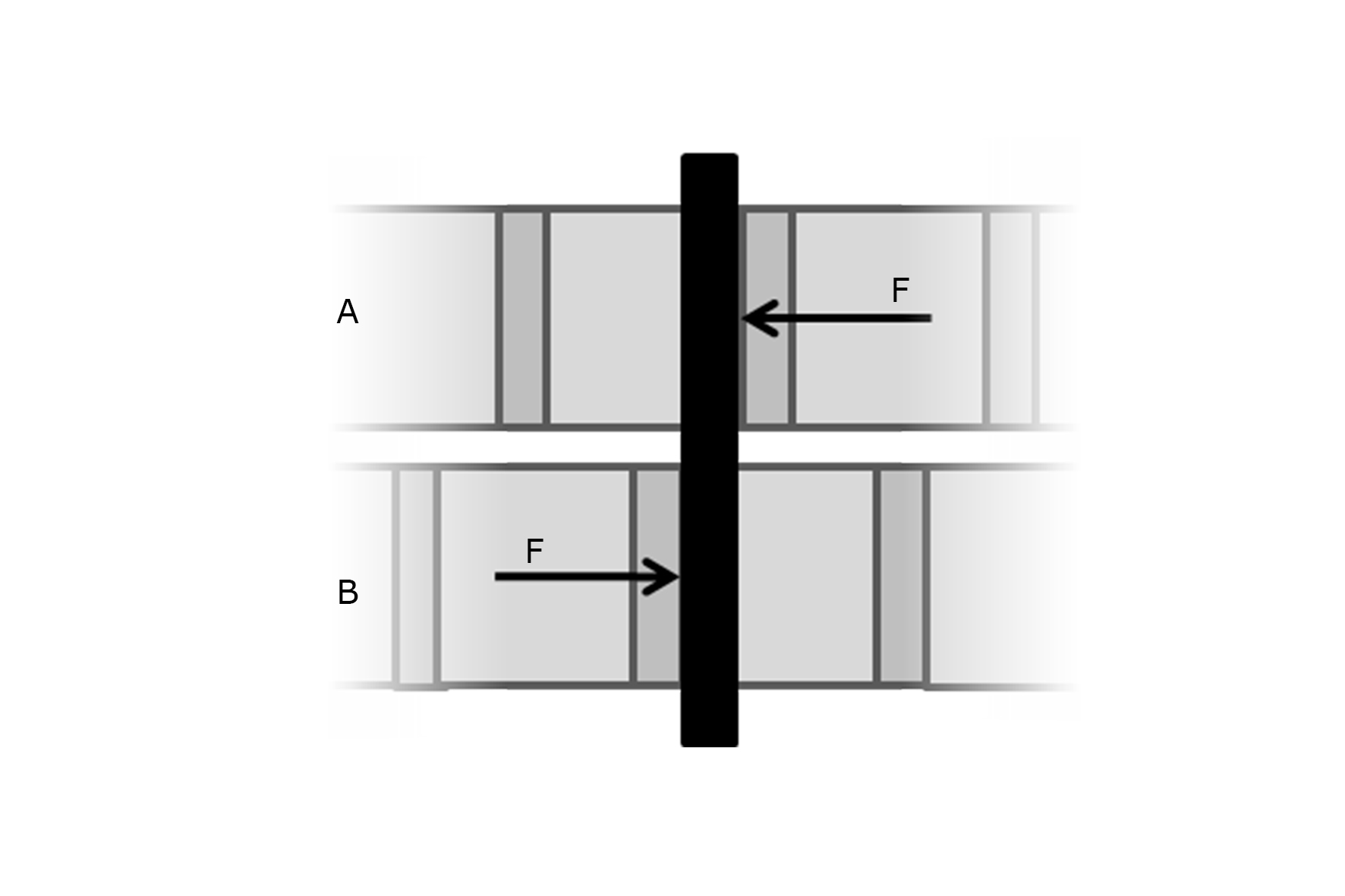
Abbildung 4: Reaktionsmoment
Von der Unterseite zeigt sich der Greifmechanismus wie in Abbildung 4 dargestellt. In der Konfiguration mit zwei Ketten A und B wirken zwei Kräfte auf ein längliches Objekt wie beispielsweise einen Ast. Daher ist ersichtlich, dass durch den außermittigen Kraftangriff ein Drehmoment um den Mittelpunkt des Kettenpaars entsteht. Diese muss von der Oberfläche beziehungsweise den Objekten auf der Oberfläche aufgenommen werden. Bei niedriger Traktion der Robotergegenseite ist eine Drehung um die Hochachse denkbar. Unter der Annahme, dass die Objekte die gesamte Fahrzeugbreite überragen, kann durch die symmetrische Scherkrafteinbringung das nach außen wirkende Moment eliminiert werden. Alternativ kann eine Erweiterung mit einer zusätzlichen, dritten Kette je Fahrzeugseite vorgesehen werden, so dass je Fahrzeugseite nur Greifkräfte ohne Momente wirken.
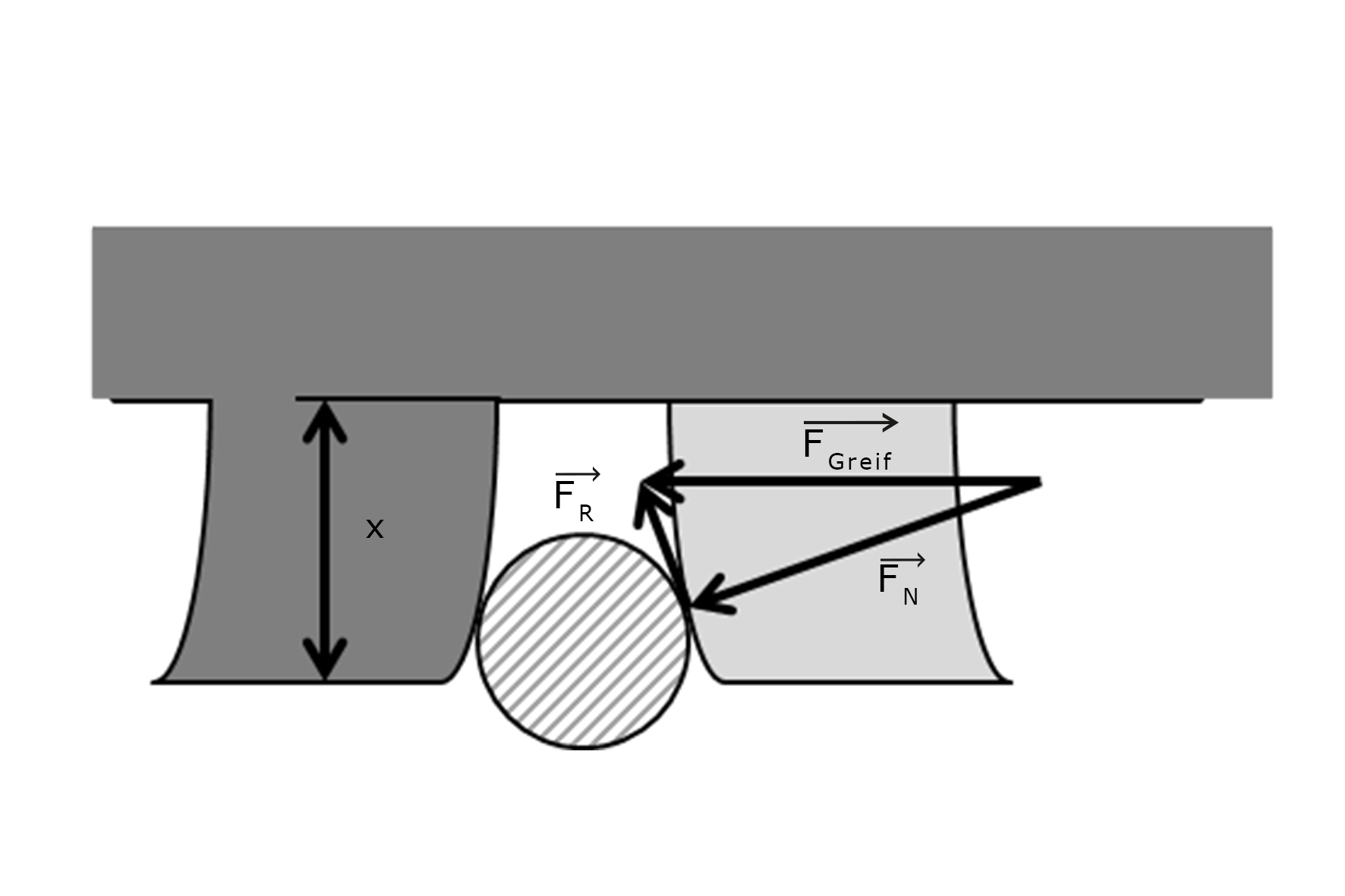
Abbildung 5: Interaktion mit Objekt
Wie in Abbildung 5 zu sehen, gestaltet sich der Greifvorgang als reibschlüssige Klemmung zwischen zwei elastischen Stegen. Über die in der Abbildung horizontale Krafteinbringung und dem verformten Steg ergeben sich eine Normalkraftkomponente und eine dazu orthogonale. Letztgenannte senkrecht stehende Kraft muss über Reibung aufgenommen werden, um das geklemmte Objekt nicht zu verlieren. Durch weitere Verformung des Kettensteges ändert sich das Verhältnis der beiden Kraftkomponenten. Ist der Winkel zu flach, wird die Haftreibungsgrenze überschritten und die Klemmung löst sich. Aus der Gleichung des Biegebalkens [12]
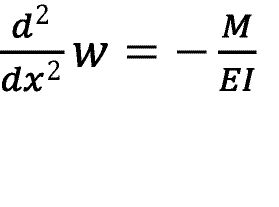
ergibt sich mit den Randbedingungen für eine einseitige feste Einspannung der maximale Winkel am Kontaktpunkt zwischen Objekt und Steg:
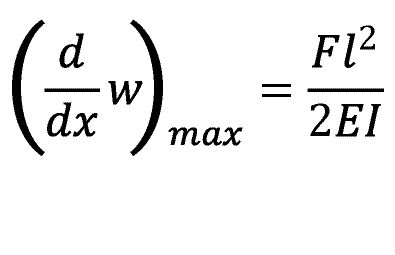
Dabei gilt für die Symbole: Verschiebung w, Greifkraft F=FGreif , Einspannlänge l , Elastizitätsmodul E und I dem Flächenträgheitsmoment. Daraus ist ersichtlich, dass die Art und Form der klemmbaren Objekte von Faktoren wie den Kettenstegabmessungen, dem Kettenwerkstoff und der Reibpaarung, beschrieben durch µ, abhängig ist. Daher könnte die Kettengeometrie auf festgelegte Objekte optimiert werden. In einer inhomogenen Umgebung ist eine Anpassung jedoch nicht möglich und wird nur ein Kompromiss sein können.
Durch die einfache Struktur ist die Adaption des hier beschriebenen Konzepts auf bestehende Plattformen prinzipiell möglich. Dies erscheint insbesondere dann sinnvoll, wenn Flipper-Ketten parallel an der Roboterseite anliegen und Einzelantriebe verbaut sind.
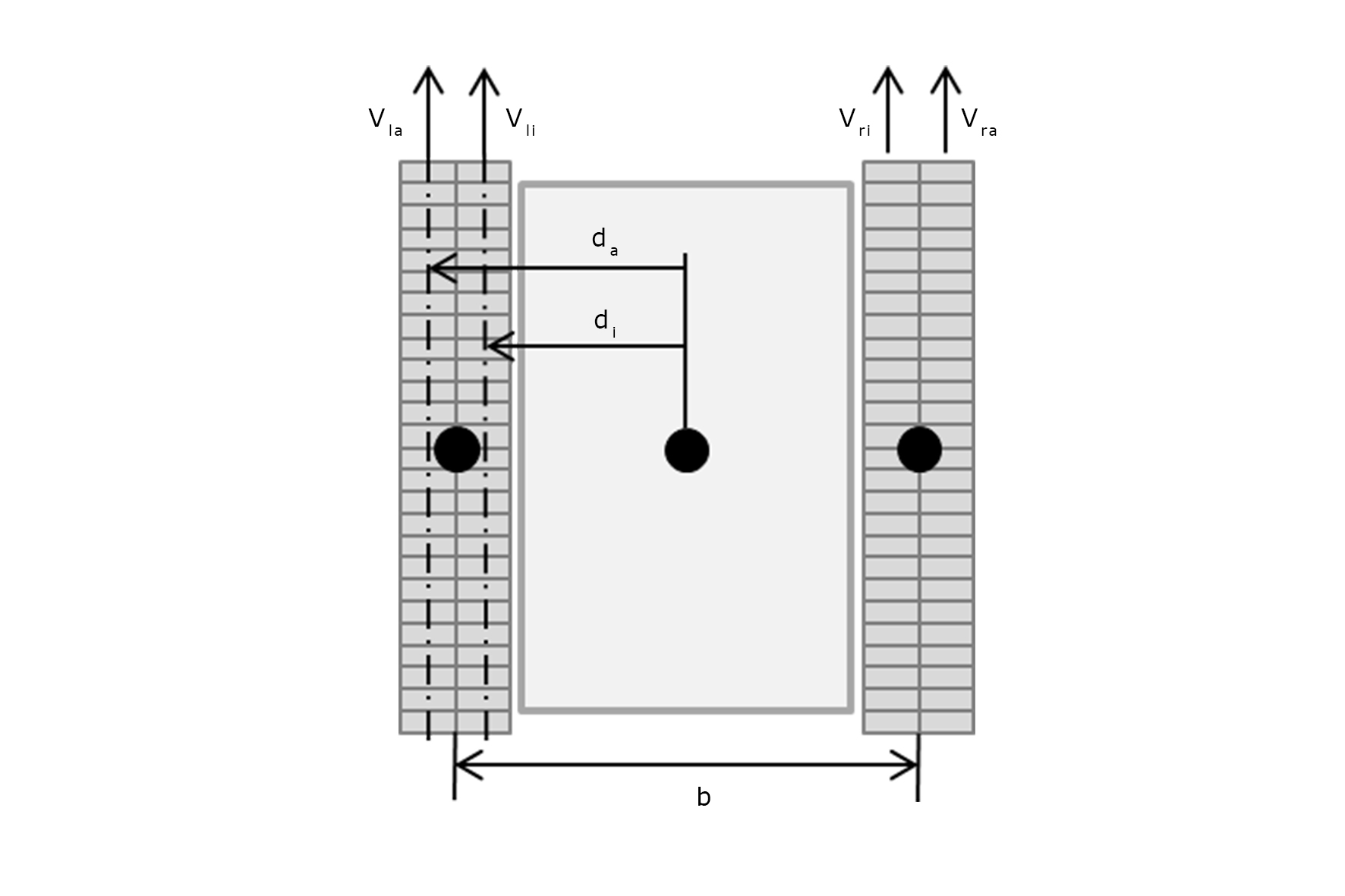
Abbildung 6: Kinematik
Um den Antrieb in herkömmliche Roboter einzubinden, werden nachfolgend Eigenheiten des Systems näher erläutert. Abbildung 6 zeigt eine schematische Darstellung in der Draufsicht des Antriebssystems. Die Größe da beschreibt den Abstand des Fahrzeugmittelpunktes zur Symmetrieebene der äußeren Kette. Entsprechend zeigt di den Abstand zur Symmetrieebene der inneren Kette. Der mittlere Kraftangriffspunkt kann in Längsrichtung mittig angenommen werden. Dadurch ergibt sich der resultierende Kraftangriffspunkt beider Ketten wie in Formel 3.7 dargestellt zu
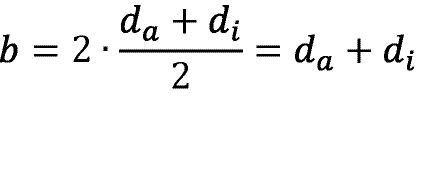
Die resultierende Geschwindigkeit einer Seite bei eingestellter Differenzgeschwindigkeit kann mit der Anzahl der Ketten n näherungsweise durch Mittelwertbildung berechnet werden.
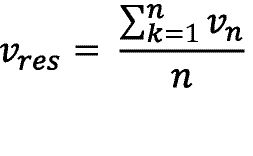
In der abgebildeten Konfiguration mit n=2 ergibt sich dann
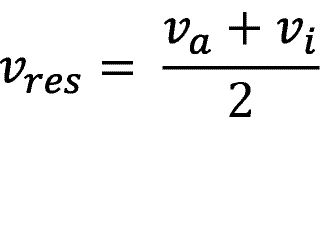
Im Falle eines geklemmten Umgebungsobjektes steigt der Strom am Antrieb der greifenden Kette und regelt die Drehzahl auf va=vi und somit die Drehzahldifferenz zu null.
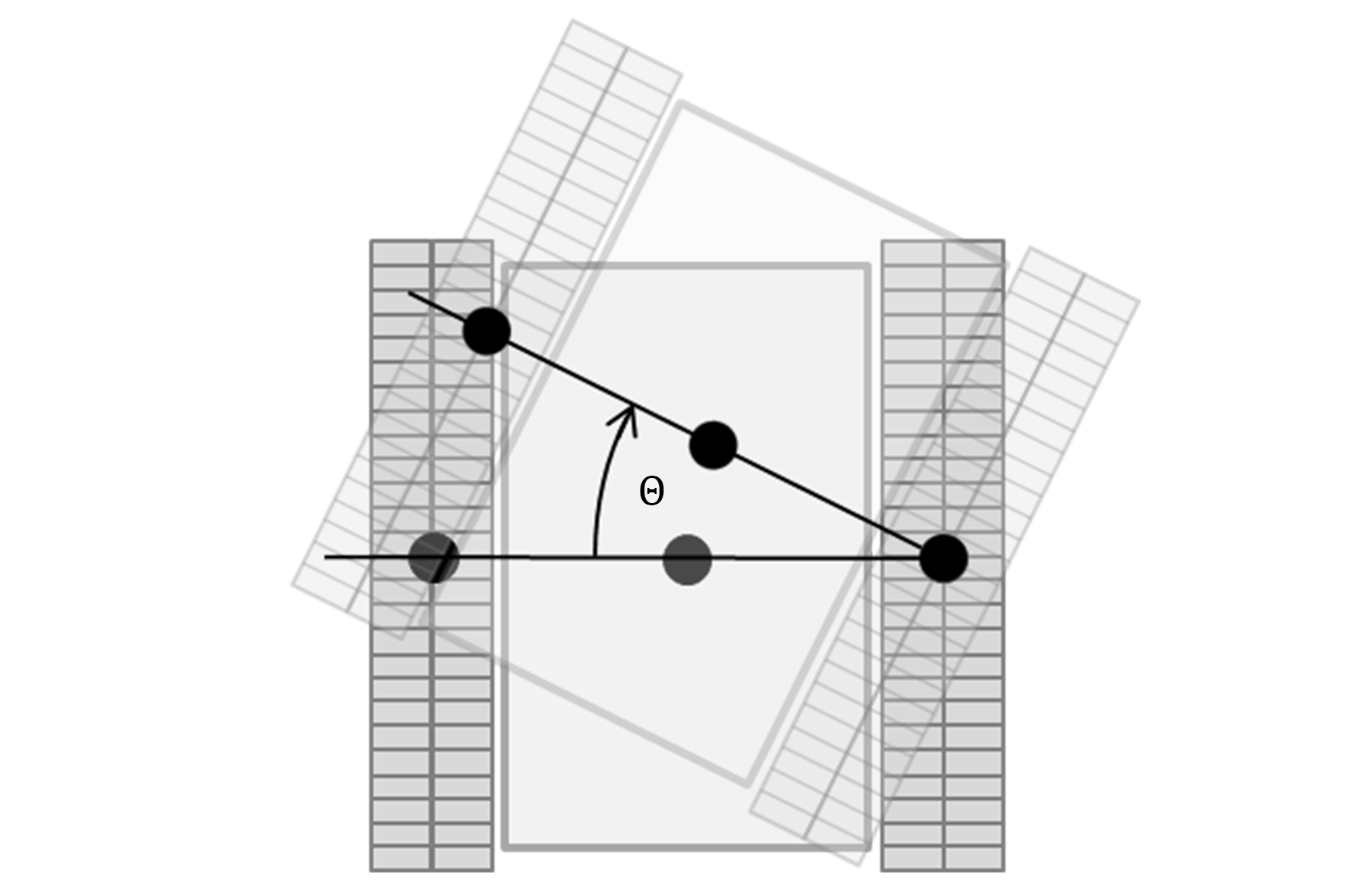
Abbildung 7: Orientierung
Für einen potentiellen Einsatz des Antriebs in bestehenden Roboterplattformen ist eine entsprechende Adaption notwendig. Diese bezieht sich wesentlich, abgesehen von mechanischen Anpassungen, auf die odometriebasierte Positionsbestimmung. Durch die getroffenen Annahmen (7) und (9) kann jedoch festgestellt werden, dass sich eine Poseermittlung mittels Odometrie ebenfalls nach herkömmlichem Verfahren berechnen lässt.
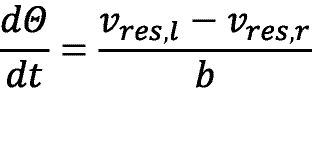
Es kann also die Veränderung der Orientierung als Differenzgeschwindigkeit der beiden Fahrzeugseiten bezogen auf die Fahrzeugbreite errechnet werden. Der Winkel der Orientierung Θ ist in Abbildung 7 ersichtlich.
4. Systembeschreibung
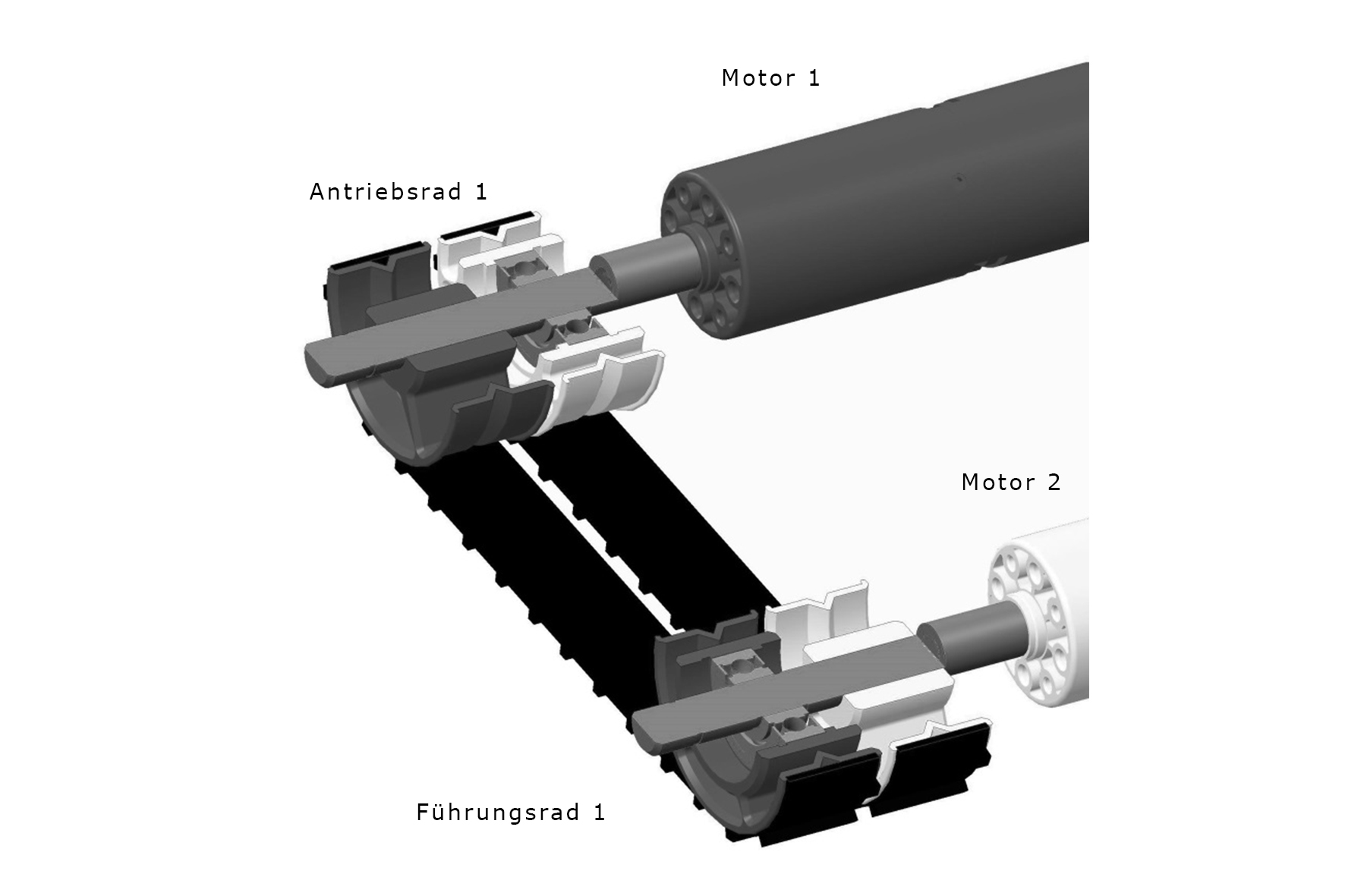
Abbildung 8: Mechanisches Grundkonzept
Auch wenn das Antriebskonzept prinzipiell mit mehreren Ketten ausgeführt werden kann, ist bei den folgenden Ausführungen von zwei Ketten auszugehen. Bei diesen zwei unabhängig steuerbaren, parallel verlaufenden Antriebsketten können die Führungs- und Antriebsräder auf einer gemeinsamen Welle sitzen. Abbildung 8 zeigt den mechanischen Entwurf. Motor 1 treibt über eine Welle ein Antriebsrad 1 an. Das Führungsrad, welches ebenfalls auf der selben Welle sitzt, wird über ein Lager von der Drehbewegung von Motor 1 entkoppelt. Umgekehrt dreht Motor 2 ebenfalls ein eigenes Antriebsrad, wobei das Führungsrad auf selbiger Welle gleichermaßen durch ein Kugellager entkoppelt ist. Diese Konstruktion ermöglicht damit zwei unabhängige Bewegungen der Ketten, welche parallel verlaufen.
Der Systementwurf (Abbildung 9) sieht eine mikrocontrollerbasierte Steuerung des Roboters vor. Es ist damit möglich, einen direkten Zugriff auf die Antriebe zu bekommen und somit drehmomentbildende Ströme und Drehzahlen zu regeln. Vorgaben können vom Leitrechner über die Schnittstelle USB➝UART übertragen werden.
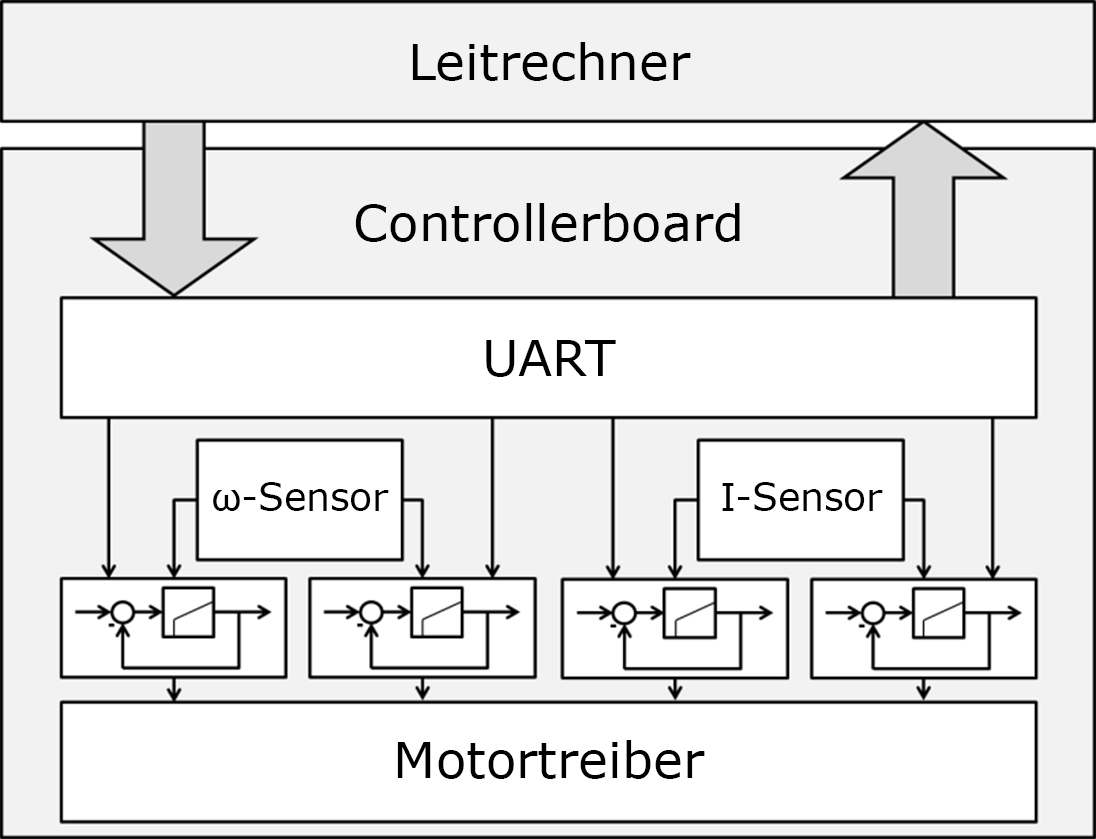
Abbildung 9: Systementwurf
Die Ansteuerung der Antriebe selbst erfolgt über Treiberbausteine, welche durch ein vom Mikrocontroller generiertes pulsweitenmoduliertes Signal gesteuert werden. Motorströme werden über den Spannungsabfall an einem Serienwiderstand erfasst und erlauben über die Verrechnung der Motorparameter eine Ermittlung des Antriebsmoments. Über den Durchmesser des Triebrades lässt sich die Kraft an den Ketten bestimmen. Drehwinkel werden durch Geber am Motorabtrieb festgestellt. Eine direkte Momenten- bzw. Kraftmessung ist nicht vorgesehen, könnte aber als Drehmomentwaage in die Motorfixierungen integriert werden.
Die Programmstruktur des Mikrocontrollers ist in Abbildung 10 gezeigt. Um eine zeitliche Koordination der Prozesse und Berechnungen sowie die Realisierung der Regelungen zu ermöglichen, ist das Controllerprogramm in Zeitscheiben aufgegliedert, welche interrupt-gesteuert aufgerufen werden. Diese Steuerung wird nach der Startsequenz, welche Initialisierungen von Unterfunktionen durchführt und Startwerte setzt, aufgerufen. Die Prozesse sind, soweit möglich, als Zustandsautomaten programmiert, um eine möglichst gleichmäßige Verteilung in den Arbeitsschritten zu erreichen.
Dabei stellen, wie in Abbildung 9 bereits dargestellt, die Abschnitte für Nachrichtenempfang und Regelung die wichtigsten Teile dar und werden entsprechend in kürzeren Intervallen aufgerufen. Dabei muss der innere Strom-Regelkreis (vgl. Abbildung 11) öfter ausgeführt werden als der äußere Drehzahlregelkreis. Nachrichtenversand zum übergeordneten Leitsystem, sowie die in Algorithmus 1 beschriebene Maximalwertsuche werden weniger oft ausgeführt, da sie als zeitunkritisch angesehen werden.
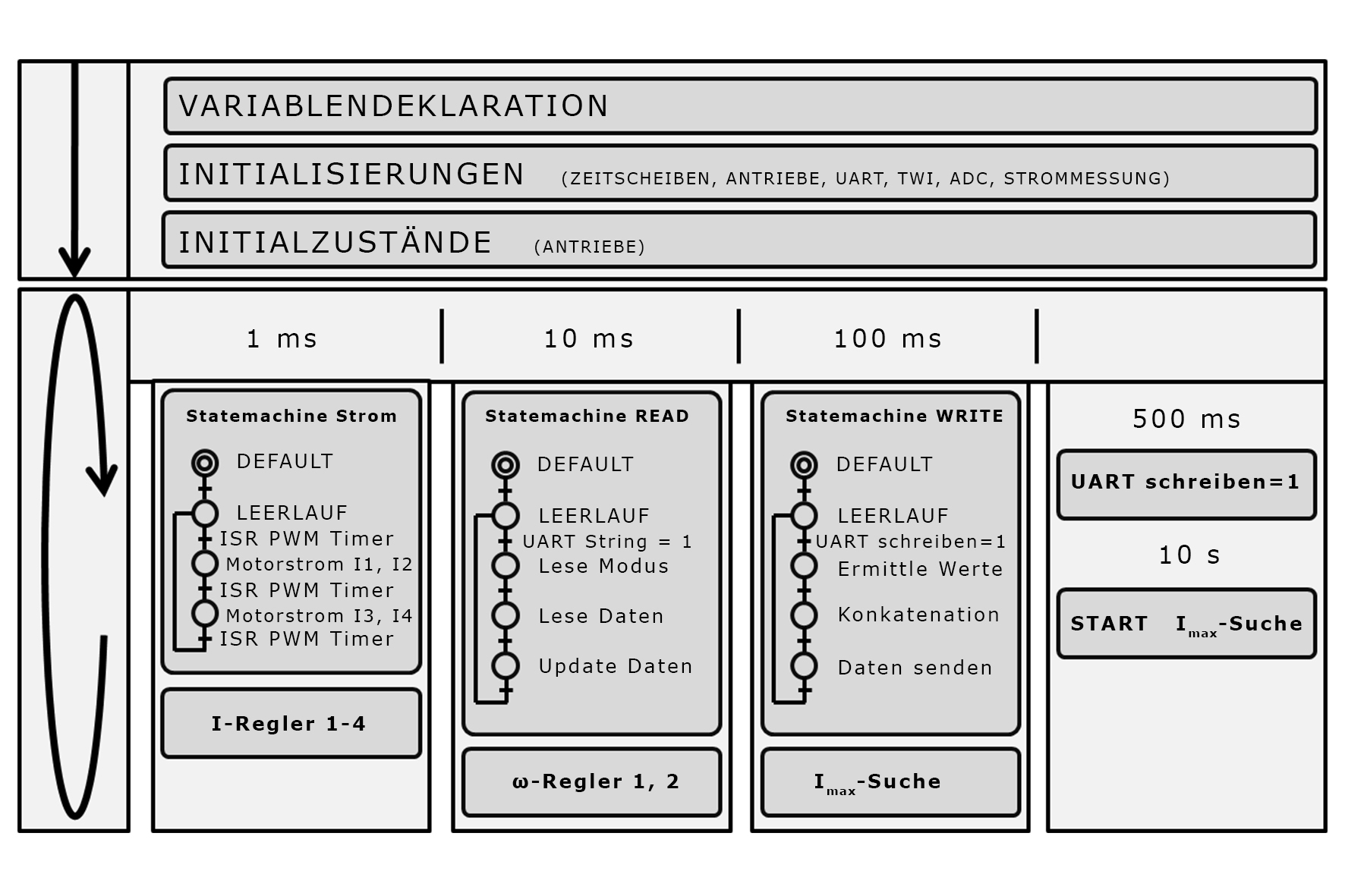
Abbildung 10: Controllerprogramm
Zur Regelung der permanenterregten Gleichstromantriebe wurde eine Drehzahl- sowie eine Momentenregelung [13] entwickelt. Die Drehzahlregelung (Abbildung 11) nach dem Stromleitverfahren gestaltet sich als Kaskadenregelung, wobei der innere Kreis den Strom und der äußere Kreis die eigentliche Drehzahl regelt.
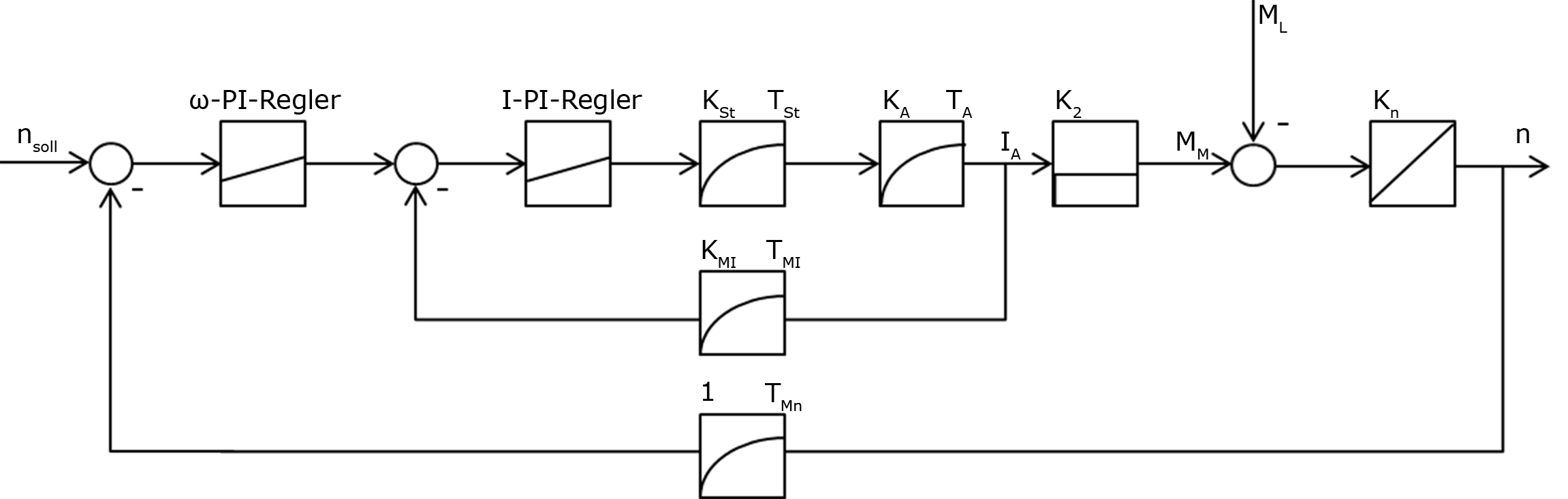
Abbildung 11: Drehzahlregelung
Die Parameter des Motorankers KA und TA können direkt aus dem Ankerwiderstand und der Induktivität bestimmt werden. Mit
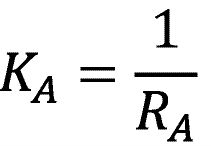
und
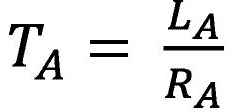
Ergibt sich als Strom-PI-Regler für eine Optimierung nach dem Betragsoptimum
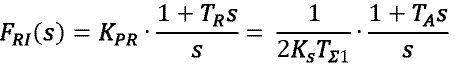
Wobei die Verstärkungen KSt und KMI mit KA multiplikativ in Ks und die Zeitkonstanten von Steller und Stromsensor in TΣ1 additiv zusammengefasst sind.
Die Konstante K2 kann als Motorkonstante aufgefasst werden. Sie ergibt sich entweder aus Messung von Drehzahl und Spannung oder aus Herstellerangaben. Sie beschreibt das Verhältnis
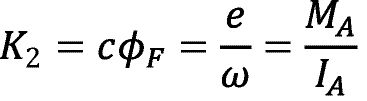
Mit konstanter Erregung, welche bei einem dauermagneterregten Kleinmotor gegeben ist, bleibt cϕF konstant und das Verhältnis von induzierter Gegenspannung zu Winkelgeschwindigkeit bzw. Ankermoment zu Ankerstrom ist gegeben.
Die Verstärkung Kn beschreibt die Trägheit des Ankers. Als Integrator errechnet sich mit dem eingeleiteten Moment die erreichte Drehzahl.
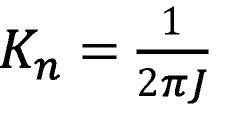
Das Trägheitsmoment J kann mittels Auslaufversuch ermittelt werden.
Wird die Stromregelung als PT1-Glied mit der Zeitkonstante 2TΣ1 und der Verstärkung 1 angenähert, kann der äußere Drehzahl-PI-Regler nach dem symmetrischen Optimum entworfen werden.
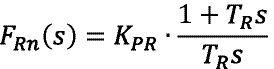
Mit der Reglerverstärkung
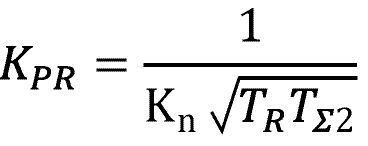
und der Zeitkonstante
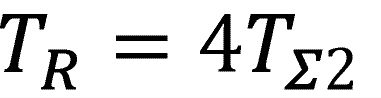
ergeben sich mit TΣ2=2TΣ1+TMn die benötigten Werte.
Der Regelkreis der momentengeregelten Antriebsgleiskette wird analog zum inneren Regelkreis der drehzahlgeregelten Kette entworfen, wobei der drehmomentbildende Strom als Regelgröße dient (Abbildung 12). Über die als K2 bezeichnete Motorkonstante ist ein festes Verhältnis zum erreichten Moment gegeben und kann daher äquivalent verwendet werden.
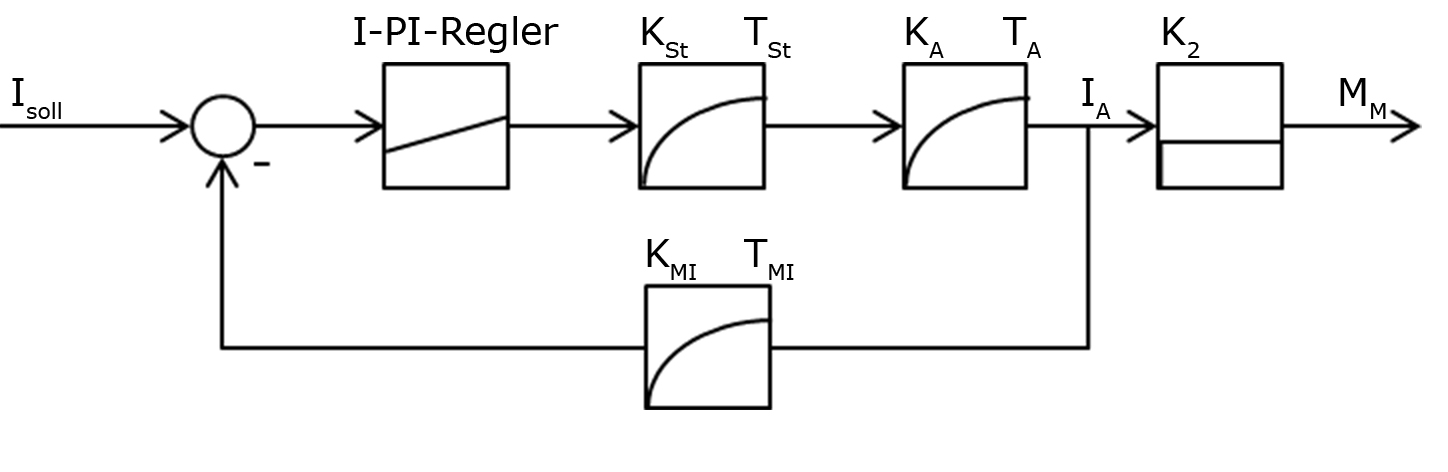
Abbildung 12: Momentregler
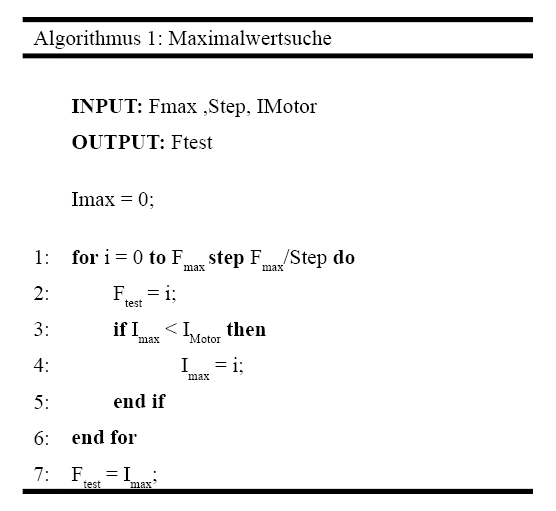
Um auf Oberflächen wechselnder Beschaffenheit ein optimales Ergebnis zu erzielen, muss der Sollwert der Momentenregelung nachgeführt werden. Dies kann per Algorithmus in regelmäßigen Abständen erfolgen (vgl. Algorithmus 1). Es wird vorausgesetzt, dass der Algorithmus parallel zum eigentlichen Programmablauf ausgeführt wird.
Für eine Abschätzung der erreichbaren Greifkraft wird der erreichte Motorstrom des klemmenden Kettenantriebs herangezogen. Weitere Eingangsgrößen sind die errechnete maximale Greifkraft und die Schrittweite, mit der die Greifsollkraft zu verändern ist. Mit jedem Aufruf wird der Sollwert der Klemmkraft schrittweise von null bis Fmax erhöht. Der Wert der Laufvariable i wird beim jeweils höchsten gemessenen Stromwert gespeichert und nach dem gesamten Durchlauf als Sollwert bis zur nächsten Suche verwendet. Dieser Wert stellt daher die Ausgangsgröße dar.
Der aufgebaute Versuchsträger ist in Abbildung 13 dargestellt. Er basiert auf den Überlegungen in diesem Beitrag und beinhaltet das in Abbildung 8 gezeigte Antriebssystem.

Abbildung 13: Griprob-Plattform
Die Pfeile markieren dabei folgende Komponenten:
1. Steuerplatine mit AVR-Controller, Motortreiber, Motorstromsensor, UART-USB-Schnittstelle, Spannungsversorgung (direkt mit der Steuerplatine verbunden sind Akkupack, Beschleunigungs- und Gierratensensor, Temperatursensor)
2. Leitrechner (durch Roboter verdeckt) mit ROS
3. Getriebemotor (treibt über Zahnriemen untenliegenden Kettenantrieb an)
4. Drehwinkelgeber (stirnseitig am Motorabtrieb)
5. zweireihiger Kettenantrieb
Gesamt ergeben sich dazu folgende Leistungsdaten (Tabelle 1):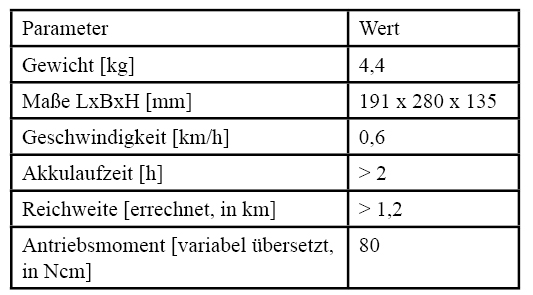
Tabelle 1: Eigenschaften
5. Ergebnisse
Zum Zeitpunkt der Veröffentlichung können noch keine umfassenden Ergebnisse dargestellt werden, weil dazu eine entsprechende Prüfeinrichtung entworfen werden muss. Ein Versuchsstand auf Grundlage des Reibversuchs (vgl. Abbildung 1) soll entsprechende Resultate liefern. Es ist vorgesehen, durch Veränderung der Neigung eines ebenen Testfeldes eine erhöhte Traktion durch den Greifmechanismus nachzuweisen. Dabei sollen Oberflächen, Kettengeometrie und Greifkräfte variiert und durch die maximale Steigfähigkeit eine Aussage über die Leistungsfähigkeit in Abhängigkeit der genannten Größen getroffen werden.
6. Diskussion
Das vorgeschlagene System erlaubt es, die Traktion eines mobilen Roboters aktiv zu erhöhen. Die entwickelten Regelungen der Antriebe bieten die Möglichkeit, sowohl Drehzahl als auch Greifkraft vorzugeben und somit zu den herkömmlichen Steuermöglichkeiten des Robotersystems die weitere Variable Greifkraft einzuführen. Damit kann auf die gezielte Erhöhung der Traktion beziehungsweise auf die Optimierung der Schnittstelle Roboter und Umgebung eingewirkt werden. Im Vergleich zu den Arbeiten, welche sich auf die optimale Identifikation und Beschreibung des Antriebselement-Umgebungskontakt beschränken und darüber Antriebsregelung und Odometrie verbessern, kann mit dem vorgeschlagenen System gezielt Einfluss auf dieses Schnittstelle genommen werden. Der Nachteil der Roboter mit unterdruckbasierter Normalkrafterhöhung, die für schweres Gelände ungünstig sind, ist hier durch einen schmutzunempfindlichen Aufbau vermieden. Artverwandte Aufbauten mit verschiedenen Kettenkonfigurationen lassen sich prinzipiell mit dem hier vorgeschlagenen System kombinieren und erweitern. Es ist zu erwarten, dass eine solche Kombination eine weitere Verbesserung des Konzepts bietet, da sich die Greifwirkung optimal entfalten kann, wenn die Ketten parallel auf dem Untergrund aufliegen.
Nachteilig bei diesem System ist die begrenzte Wirksamkeit auf trockenen, sandigen Böden, da diese im Vergleich zu bewachsenen oder mit Wurzeln durchsetzten Oberflächen nur geringe Scherkräfte aufnehmen können und zur Verschiebung neigen. Daher ist die Wirksamkeit des Mechanismus in diesen Bereichen beschränkt. Es ist jedoch möglich, die Greifkette als reguläre Antriebskette zu schalten, so dass sich gegenüber herkömmlichen Antrieben kein Nachteil ergibt.
Wie in Gleichung 3.4 beschrieben, wird nicht die komplett zur Verfügung stehende Leistung in Vortrieb umgesetzt, da ein Teil für die Greifkräfte aufgewendet werden muss. Insofern ist dieser Punkt aus Sicht der Reichweite des Fahrzeugs interessant. Ohne Greifsystem sind durchaus höhere Reichweiten erreichbar, allerdings entspricht die in diesem Fall erreichbare Traktion den herkömmlichen Konzepten. Hierbei können die Ketten synchron betrieben werden, so dass der Greifprozess deaktiviert ist. Daher scheint diese Möglichkeit ein Anknüpfungspunkt für weitere Arbeiten, der die Traktion auch aus energetischer Sicht optimieren würde.
Des Weiteren ist die Erarbeitung einer Testumgebung und der Bestimmung von Testparametern erforderlich, um die entworfenen Regelungen zu optimieren und deren Leistungsfähigkeit zu beschreiben.
Erklärung zu möglichen Interessenkonflikten
Die Autoren erklären, dass in Zusammenhang mit der vorliegenden Arbeit keinerlei Interessenkonflikt besteht.
7. Literatur
[1] Xie, S.; Bao, S.; Zou, B.; Pu, H.; Luo, J.; Gu, J. (2013): The research on obstacle-surmounting capability of six-track robot with four swing arms. In: Proceedings of the 2013 IEEE International Conference on Robotics and Biomimetics (ROBIO), S. 2441–2445.
[2] Choi, Y.; Jeong, K.; Kang, J.; Seo, Y.; Lee, S.-U. (2007): A remotely operated mobile robot with modular track mechanisms. In: Proceedings of the 2007 IEEE International Conference on Control, Automation and Systems (ICCAS ‚07), S. 1002–1005.
[3] Zong, C.; Jiang, S.; Guo, W.; Li, L.; Gao, X. (2014): Obstacle-surmounting capability analysis of a joint double-tracked robot. In: Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation (ICMA), S. 723–728.
[4] Dooyeol, K.; Hyunghak, H.; Soohyun, K. (2009): Design of multi-joint tracked robot for adaptive uneven terrain driving. In: Proceedings of the 4th International Conference on Autonomous Robots and Agents, Feb 10-12, 2009, Wellington, New Zealand, S. 464–469.
[5] Li, Z.; Ma, S.; Li, B.; Wang, M.; Wang, Y. (2009): Parameter design and optimization for mobile mechanism of a transformable wheel-track robot. In: Proceedings of the 2009 IEEE International Conference on Automation and Logistics. ICAL ‚09 ; 5 - 7 Aug. 2009, Shenyang, China. Piscataway, NJ: IEEE, S. 158–163.
[6] Ojeda, L.; Cruz, D.; Reina, G.; Borenstein, J. (2006): Current-Based Slippage Detection and Odometry Correction for Mobile Robots and Planetary Rovers. In: IEEE Transactions on Robotics 22 (2), S. 366–378.
[7] Brooks, C. A.; Iagnemma, K. (2012): Self-supervised terrain classification for planetary surface exploration rovers. In: Journal of Field Robotics 29 (3), S. 445–468. DOI: 10.1002/rob.21408.
[8] Al-Milli, S.; Seneviratne, L. D.; Althoefer, K. (2010): Track–terrain modelling and traversability prediction for tracked vehicles on soft terrain. In: Journal of Terramechanics 47 (3), S. 151–160.
[9] Dos Santos, A.J.V.; Silva, A.F.C.; da Rocha Souto, C.; da Silva, S. A.; Lima, A.M.M. de: Detecting soil parameters from a small tracked vehicle. In: Proceedings of the 2015 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), S. 1446–1451.
[10] Parness, A. (2011): Anchoring foot mechanisms for sampling and mobility in microgravity. In: Proceedings of the 2011 IEEE International Conference on Robotics and Automation, May 9-13, 2011, Shanghai, China, S. 6596–6599.
[11] Bekker, M. G. (1956): Theory of Land Locomotion. The mechanics of vehicle mobility: University of Michigan Press.
[12] Gross, D.; Hauger, W.; Schröder, J.; Wall, W. A. (2007): Technische Mechanik (Gross, D.). Band 2: Elastostatik. 9., vollst. neu bearb. Aufl. Berlin: Springer Vieweg (Springer-Lehrbuch).
[13] Schulz, G. (2010): Regelungstechnik 1. Lineare und Nichtlineare Regelung. Rechnergestützter Reglerentwurf. 4., überarbeitete Auflage. München: Oldenbourg.

Dipl.-Ing. (FH) Ludwig Barthuber, M.Eng.
Ludwig Barthuber schloss eine Berufsausbildung zum Prozessleitelektroniker ab, bevor er ein Diplom-Studium des Maschinenbaus an der Hochschule in Deggendorf absolvierte. Nach vielfältigen Projekttätigkeiten als Laboringenieur in verschiedenen Einrichtungen der Hochschule begann er sein Master-Studium in Mechatronik (M.Eng.) und schloss dieses im Frühjahr 2012 ab. Barthuber ist Doktorand der Universität Würzburg im Bereich Robotik.
Ludwig Barthuber completed a professional training as a process control electrician before he graduated with a diploma degree in mechanical engineering at Deggendorf Institute of Technology. After various project activities as laboratory engineer at several departments of DIT, he began his Master studies in mechatronics (M.Eng.), which he completed successfully in spring 2012. Barthuber currently is a doctoral student at Würzburg University, where he prepares his dissertation in the field of robotics.
Kontakt / Contact:

Prof. Dr.-Ing. Peter Firsching
Prof. Dr.-Ing. Peter Firsching ist seit 2001 Professor für Elektrische Maschinen und Antriebe an der Technischen Hochschule Deggendorf. Dort vertritt er weiterhin die Lehrgebiete Steuerungs- und Automatisierungstechnik, Robotik sowie Modellbildung und Simulation. Als Leiter des Technologie Campus für Mechatronische Systeme in Cham koordiniert er F&E-Aktivitäten im Bereich der mechatronischen Prozessoptimierung. Sein F&E-Schwerpunkt ist der flexible Einsatz von Robotersystemen in der Produktion.
Prof. Dr.-Ing. Peter Firsching is a professor for electric machines and drives at the Deggendorf Institute of Technology. Furthermore he is responsible for the fields of teaching control and automation engineering, robotics and Modelling and Simulation. As head of the Technology Campus of Mechatronic Systems in Cham he coordinates R & D activities in the field of mechatronic process optimization. His R&D focus is the field “Flexible use of robot systems in production”.
Kontakt / Contact:
