Efficiency Improvement of Energy Harvesting Circuits by High Q Matching
DOI Nr.: https://doi.org/10.25929/aqcz-4z34
Christian Merz
Technische Hochschule Deggendorf
Gerald Kupris
Technische Hochschule Deggendorf
ABSTRACT
Unter RF Energy Harvesting versteht man die Gewinnung geringer Energie aus einem elektromagnetischen Feld. Diese Energie kann benutzt werden, um ein kleines Mikrosystem, wie z. B. ein draht- und batterieloses Sensorsystem, zu versorgen. An der Technischen Hochschule Deggendorf ist ein derartiges RF Energy Harvesting System entwickelt und getestet worden. Diese Publikation beschreibt die einzelnen Schaltblöcke des RF Energy Harvesting Systems und zeigt eine explizite Möglichkeit auf, das System zu verbessern. Die Methode beruht auf der Verwendung von Anpassungsnetzwerken mit besonders hoher Güte (High-Q-Matching), welche die Gesamteffizienz von RF Energy Harvesting Systemen erhöhen. Anstatt herkömmliche Induktivitäten und Kapazitäten als Anpassungselemente zu verwenden, werden Elemente mit hoher Güte, wie z. B. Akustische-Oberflächenwellen-Resonatoren, benutzt. Verschiedene High-Q- und Low-Q-Anpassungsnetzwerke werden in dieser Arbeit simuliert und ihre Vor- und Nachteile diskutiert.
RF energy harvesting is the extraction of small amounts of energy from an electromagnetic field. This energy can be used to power a tiny microsystem like a wireless and battery-less sensor. At Deggendorf Institute of Technology we have constructed and tested a RF energy harvesting circuit. This paper describes the building blocks of an RF energy harvesting system and explicitly discusses a possibility of improving the system. The method deals with high Q matching circuits that increase the overall efficiency of RF energy harvesting circuits. Instead of common inductive and capacitive matching elements, high Q elements such like surface acoustic wave resonators are used. Different high Q and low Q matching circuits are simulated in the paper and their advantages and disadvantages are discussed.
KEYWORDS
High-Q-Matching, SAW-Resonator, Effizienzsteigerung von Energy Harvesting Schaltungen, RF Energy Harvesting
1. Einleitung und theoretische Grundlagen
1.1 RF Energy Harvesting
Unter Energy Harvesting versteht man die Gewinnung kleiner Mengen von elektrischer Energie aus Quellen wie z. B. Temperaturgradienten, Vibrationen, Luftströmungen, Sonnenenergie, Druckunterschieden oder elektromagnetischen Wellen [1]. Mit der gewonnenen Energie ist es möglich, mobile Geräte mit geringer Leistung zu versorgen. Die Energiegewinnung aus elektromagnetischer Strahlung wird als RF Energy Harvesting bezeichnet. An der Technischen Hochschule Deggendorf läuft derzeit ein Projekt, in dem ein draht- und batterieloses Sensorsystem entwickelt wurde, welches seine Versorgungsenergie aus elektromagnetischen Wellen bezieht. Das Sensorsystem arbeitet bei einer Frequenz von 868 MHz, da dieses Frequenzband von der Bundesnetzagentur freigegeben ist. In einer früheren Publikation [2] der Autoren ist ein RF Energy Harvesting System vorgestellt worden, welches bei einer einer minimalen Eingangsleistung von -6 dBm am Ausgang eine Energie von ca. 50 µJ erzeugen kann, welche ausreicht, um das entwickelte Sensorsystem zu versorgen. Das folgende Blockschaltbild zeigt beispielhaft eine vereinfachte Darstellung der Bestandteile eines RF Energy Harvesting Systems.
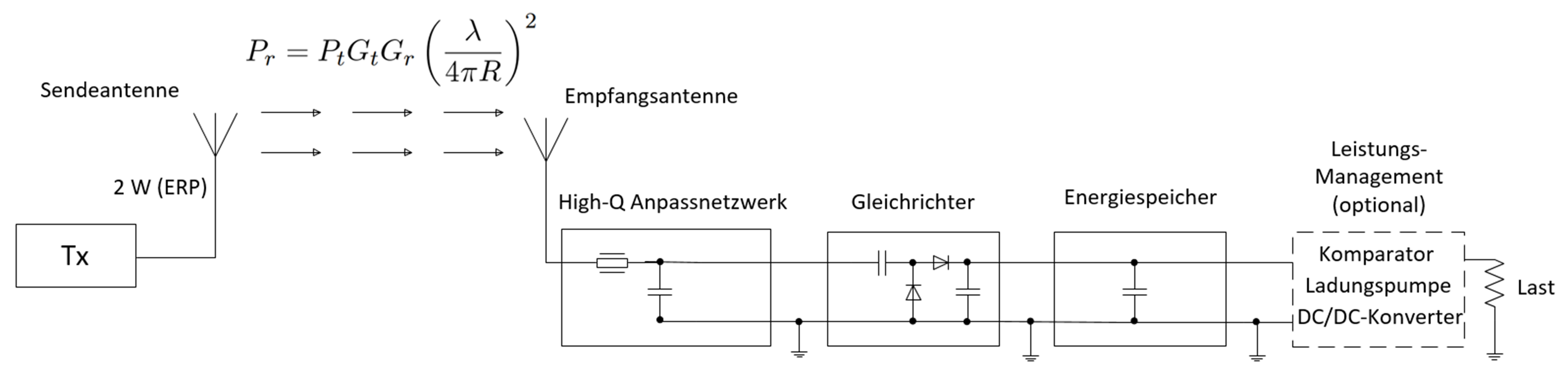
Abb. 1: Beispiel eines RF Energy Harvesting Systems
Das Funktionsprinzip des RF Energy Harvesting Systems wird im Folgenden kurz erklärt. Ein Signalgenerator sendet eine elektromagnetische Welle im 868 MHz Band mit einer Leistung von 2 W (ERP) über eine Sendeantenne ab. Diese Welle wird beim Harvester über eine Empfangsantenne empfangen und durch ein Gleichrichternetzwerk (z. B. kaskadierte Greinacher-Schaltung) gleichgerichtet. Das Anpassungsnetzwerk sorgt dafür, dass am Eingang des Harvesters die Signalreflexionen minimiert werden und die übertragene Leistung maximiert wird. Die gleichgerichtete Energie wird anschließend in einem Ladekondensator zwischengespeichert und über ein Energiemanagement (z. B. bestehend aus einem Komparator und einem DC/DC-Konverter) aufbereitet. Das aufbereitete Signal (z. B. pulsierende Gleichspannung) wird verwendet, um eine Last (z. B. ein Sensorsystem) zu versorgen.
Die detaillierte Funktionsweise des in Abbildung 1 dargestellten RF Energy Harvesting Systems wird in [2] detailliert beschrieben.
Der Hauptunterschied zwischen dem dort beschriebenen System und dem neuen System in Abbildung 1 besteht darin, dass die Güte des Anpassungsnetzwerks erhöht worden ist. Im Folgenden wird beschrieben, wie diese Erhöhung realisiert werden kann.
1.2 Impedanzanpassung mit diskreten Blindelementen in L-Topologie
Bei einem RF Energy Harvesting System ist ein Anpassungsnetzwerk notwendig, um die an der Empfangsantenne eingespeiste Leistung optimal an die restliche Schaltung übertragen zu können und um Signalreflexionen am Eingang des Harvesters zu minimieren. Das Ziel bei einer Anpassung besteht darin, die Gesamtimpedanz der RF Energy Harvesting Schaltung an die Impedanz der Empfangsantenne, welche in der Regel 50 Ω ist, anzupassen, wodurch die Leistungsübertragung maximiert wird und keine Signalreflexion am Eingang stattfindet.
Die Impedanzanpassung kann z. B. durch Stichleitungen oder durch Parallel- bzw. Serienschaltungen von zueinander konjugiert komplexen Blindelementen (z. B. Induktivität und Kapazität) erfolgen. Im Folgenden wird auf die Anpassung mit diskreten Blindelementen eingegangen.
In der Praxis werden hauptsächlich drei verschiedene Anpassungsstrukturen verwendet. Mit ihnen kann man jede beliebige Schaltungsimpedanz an die Antennenimpedanz anpassen. Die Schaltungen heißen L-, T- oder Pi-Struktur. Der Name wird vom Aussehen der Bauteilanordnung abgeleitet. [3]
Beispiele der drei Strukturen sind in den folgenden Abbildungen dargestellt.
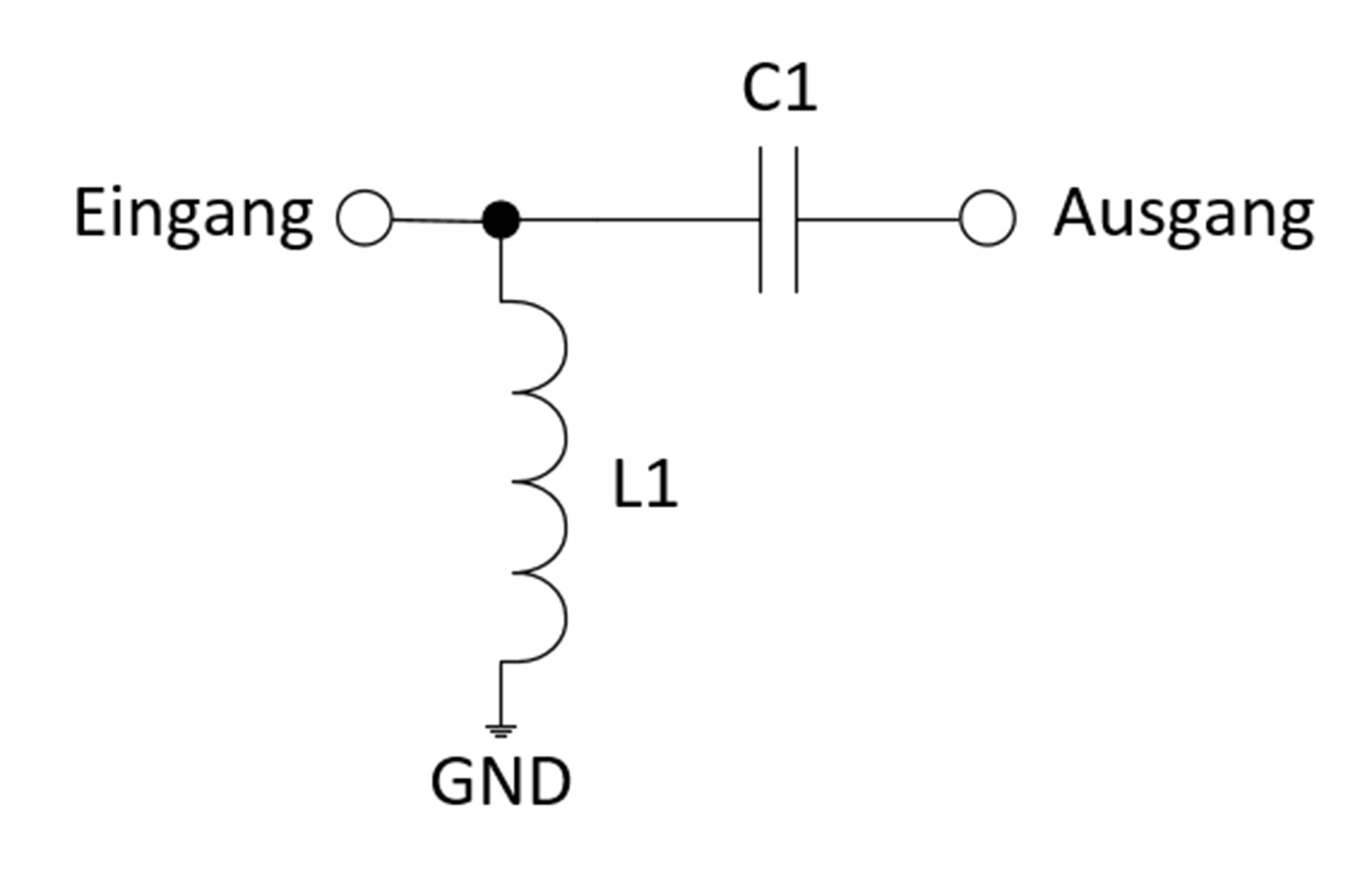
Abb. 2: Beispiel für eine L-Anpassungsstruktur
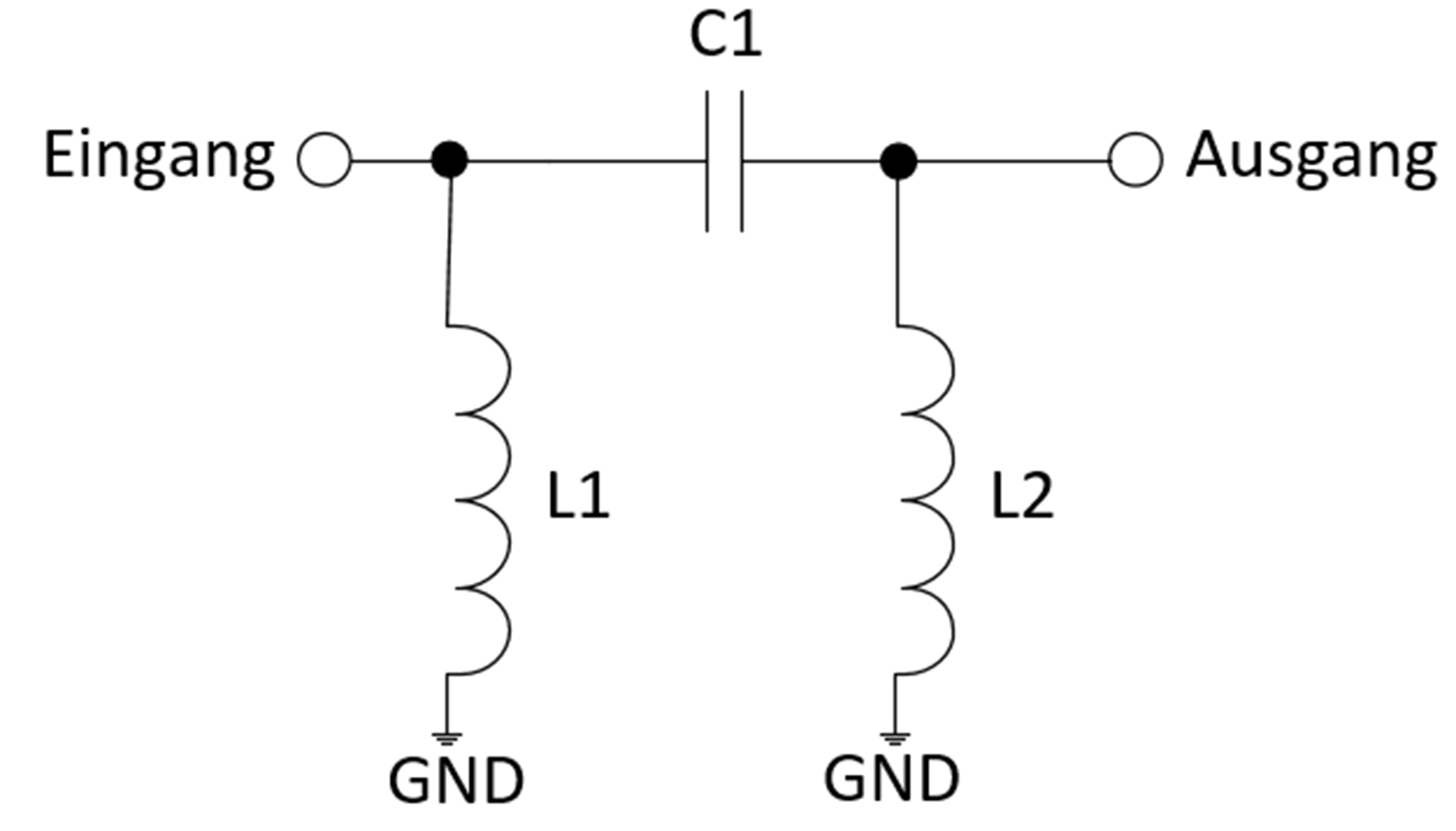
Abb. 3: Beispiel für eine Pi-Anpassungsstruktur
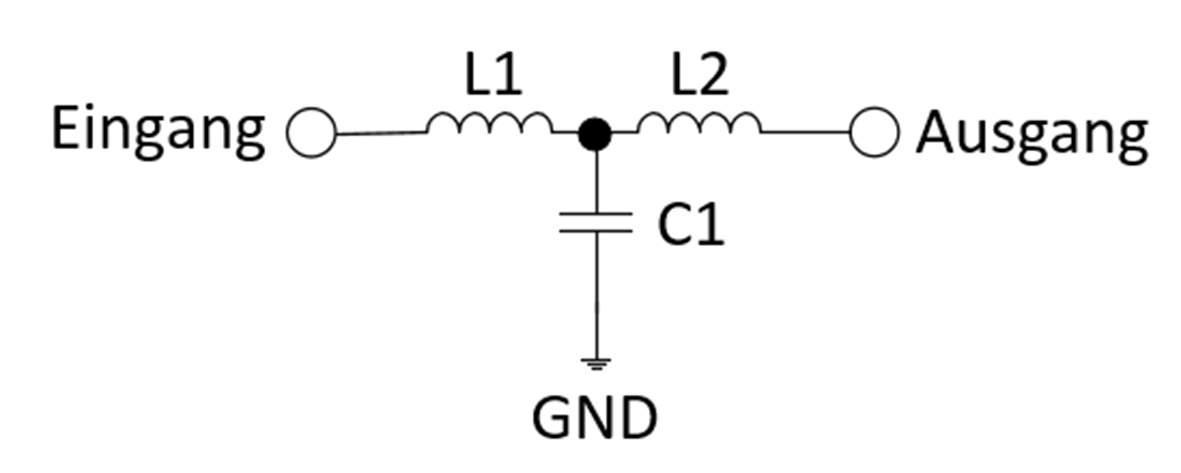
Abb. 4: Beispiel für eine T-Anpassungsstruktur
Die Anordnung der Blindelemente wird von der jeweiligen Anwendung bestimmt. Verfügt die Versorgungsspannung beispielsweise über einen unerwünschten Gleichanteil, sollte ein Kondensator in Reihe verwendet werden, der die Gleichspannung blockiert.
Ein sehr wichtiger Faktor der Anpassung stellt der Gütefaktor (engl. Q factor) dar. Dieser ist in der Elektrotechnik ein Maß für die Dämpfung eines schwingungsfähigen Systems. Man unterscheidet zwischen der belasteten Güte (engl. loaded Q or circuit Q) und der unbelasteten Güte (engl. unloaded Q or component Q). Die belastete Güte ist die Güte des gesamten belasteten Netzwerks und die unbelastete Güte ist die Güte eines Blindelements (Induktivität bzw. Kapazität) oder eines Zweigs in einem Schwingkreis.
Die L-Anpassungsstruktur ist die einfachste Anpassungsschaltung, da sie nur zwei zueinander konjugiert komplexe Bauelemente (z. B. ideale Spule und ideale Kapazität) benötigt.
Im Folgenden soll ein Beispiel für eine Anpassung mit diskreten Blindelementen mit einer L-Anpassungsstruktur aufgezeigt werden.
Die nachfolgende Abbildung zeigt ein L-Anpassungsnetzwerk für den Fall, dass der Parallelwiderstand RP größer ist als der Serienwiderstand RS.
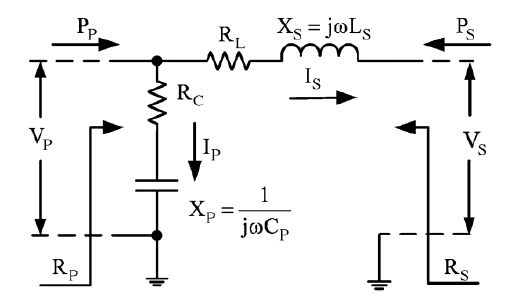
Abb. 5: Beispiel für ein L-Anpassungsnetzwerk
(Rs < Rp) [4]
Die eingezeichneten Größen haben die folgende Bedeutung:
- RC: Serienwiderstand der Kapazität CP
- RL: Serienwiderstand der Induktivität LS
- XP: Blindwiderstand der Kapazität CP
- XS: Blindwiderstand der Induktivität LS
- VP: Spannung am Parallelzweig
- VS: Spannung am Serienzweig
- RP: Parallelwiderstand
- RS: Serienwiderstand
- PP: Leistung am Parallelzweig
- PS: Leistung am Serienzweig
- IP: Strom durch den Parallelzweig
- IS: Strom durch den Serienzweig
Für das Verhältnis zwischen Parallel- und Serienwiderstand soll gelten:
(1) 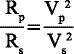
Die unbelastete Güte des Serienzweigs ist definiert als:
(2) 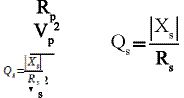
Für die unbelastete Güte des Parallelzweigs gilt:
(3) 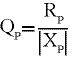
Die Spulengüte ist:
(4) 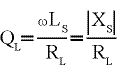
Die Komponentengüte der Kapazität ist:
(5) 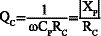
Für die belastete Güte des Netzwerks ergibt sich:
(6) 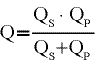
Nach Gleichung 6 dominiert bei einem L-Anpassungsnetzwerk der kleinste Gütefaktor im System. Für eine optimale Anpassung der Impedanzen sollten deshalb die unbelasteten Gütefaktoren QS und QP gleich sein.
Falls dies der Fall ist, gilt nach [5]:
(7) 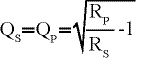
Für die Leistungen am Serien- bzw. Parallelzweig gelten die Gleichungen:
(8) 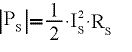
(9) 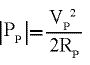
Die gesamte Verlustleistung des Anpassungsnetzwerks Ploss ergibt sich aus der Summe der beiden Verlustleistungen an der Spule (PlossL) und der Kapazität (PlossC).
Die Verlustleistungen PlossL und PlossC lassen sich wie folgt berechnen:
(10) 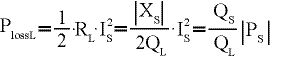
(11) 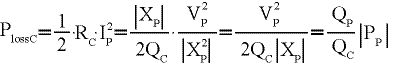
Die Leistung am Parallelzweig kann man folgendermaßen ausdrücken, wenn der rechte Anschluss des Anpassungsnetzwerks mit der Last, und der linke Anschluss mit der Signalquelle verbunden wird:
(12) 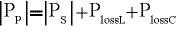
Aus den Gleichungen 10, 11 und 12 folgt somit für den Wirkungsgrad des Anpassungsnetzwerks die folgende Gleichung:
(13) 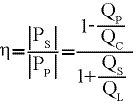
Wenn QS/QL und QP/QC << 1 gilt, wird der Wirkungsgrad sehr hoch. In der Praxis liegt die Güte einer Kapazität im besten Fall bei einigen Tausend. Die Spulengüte ist jedoch auf etwa 200 begrenzt.
Daher gilt in der Praxis oft QL << QC.
Damit lässt sich die Gleichung 13 folgendermaßen vereinfachen:
(14) 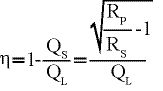
Die Gleichung 14 zeigt, dass der Wirkungsgrad des Anpassungsnetzwerks maßgeblich von der Spulengüte QL abhängt. Um die Effizienz einer Anpassungsschaltung zu vergrößern, sollte die Spulengüte erhöht werden.
Idealerweise sollte die Komponentengüte im Bereich von einigen Tausend liegen. Induktivitäten mit derart hohen Komponentengüten sind in der Praxis als diskrete Bauelemente nicht umsetzbar. Im nächsten Abschnitt wird das Konzept erläutert, wie man eine Induktivität mit hoher Spulengüte (QL > 1000) realisieren kann.
1.3 Impedanzanpassung mit SAW- bzw. BAW-Resonatoren
Eine Forschungsgruppe der Universität Freiburg hat im Jahr 2009 ein Konzept vorgestellt, bei dem ein Schwingquarz bei einer Frequenz von 24 MHz als eine Induktivität mit einer Komponentengüte von 81700 realisiert worden ist [6].
Schwingquarze haben eine Resonanzfrequenz von bis zu 300 MHz und können über eine unbelastete Güte von über 80000 verfügen.
Für RF Energy Harvesting Schaltungen, die kommerziell eingesetzt werden sollen, sind vor allem die Frequenzbänder von 868 MHz und 2,4 GHz interessant, da diese von der Bundesnetzagentur freigegeben sind und die höchsten Sendeleistungen von 2 Watt (ERP) bzw. 4 Watt (EIRP) abgestrahlt werden dürfen und die Reichweite der Energieübertragung somit bei weitem höher ist. Bei niedrigeren ISM-Frequenzen, z. B. bei 169 MHz, sind jedoch nur 10 mW (ERP) Abstrahlleistung erlaubt. Da für das vorgestellte RF Energy Harvesting System eine Frequenz im 868 MHz Band verwendet werden soll, sind Schwingquarze für eine High-Q-Anpassung ungeeignet.
Für Resonanzfrequenzen zwischen 300 MHz und 1 GHz eignen sich SAW (Surface Acoustic Wave)-Resonatoren. Diese können eine unbelastete Güte von über 8000 haben.
Bei Resonanzfrequenzen von über 1 GHz eignen sich BAW (Bulk Acoustic Wave)-Resonatoren. Diese erreichen einen unbelasteten Gütefaktor von über 1000 und unterscheiden sich von SAW-Resonatoren dadurch, dass die Ausbreitung der akustischen Welle im Substrat (Bulk) anstatt an der Oberfläche erfolgt. Wenn man einen SAW- bzw. BAW-Resonator zwischen der Serienresonanzfrequenz und der Parallelresonanzfrequenz betreibt, hat dieser ein induktives Verhalten und kann somit als Induktivität hoher Güte betrachtet werden.
Das Ersatzschaltbild eines SAW- bzw. BAW-Resonators ist in der folgenden Abbildung dargestellt.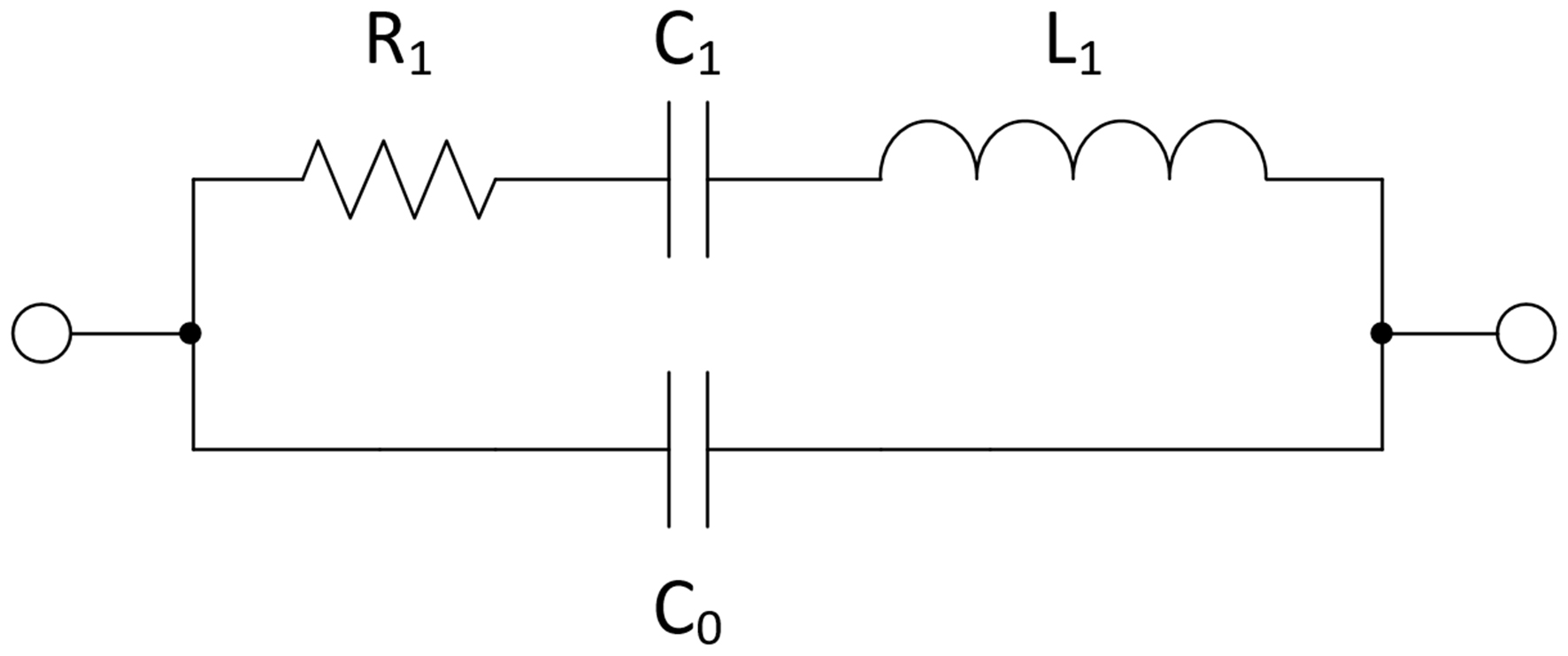
Abb. 6: Ersatzschaltbild eines SAW- bzw. BAW-Resonators
Die dynamische Kapazität C1, die dynamische Induktivität L1 und der Resonanzwiderstand R1 bilden einen verlustbehafteten Serienresonanzschwingkreis. Die statische Kapazität C0 ist die an den Anschlüssen des Resonators unmittelbar messbare Kapazität, die zusammen mit L1 und C1 einen Parallelresonanzschwingkreis bildet. Die folgende Abbildung zeigt das Blindwiderstandsdiagramm eines SAW-Resonators.
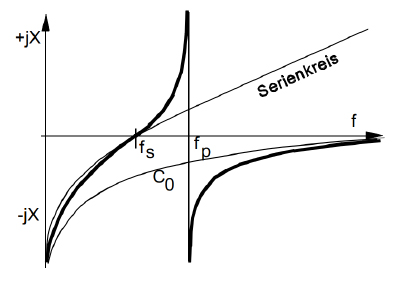
Abb. 7: Blindwiderstandsdiagramm eines SAW-Resonators [7]
Wie man aus dem Diagramm entnehmen kann, erscheint der Schwingkreis zwischen der Reihenresonanzfrequenz fs und der Parallelresonanzfrequenz fp rein induktiv.
Die Reihenresonanzfrequenz kann man wie folgt berechnen:
(15) 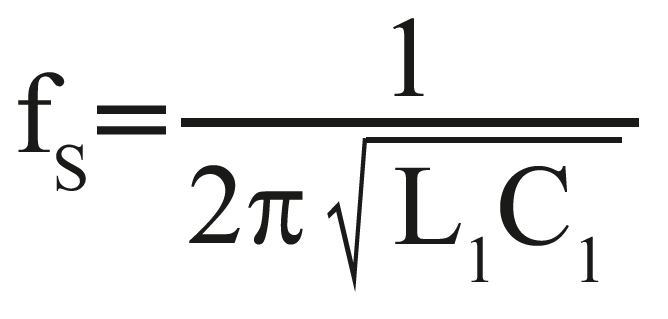
Die Parallelresonanzfrequenz ist:
(16) 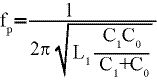
Für die effektive Induktivität eines SAW-Resonators ergibt sich:
(17) 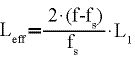
1.4 Vorteile des High-Q-Matchings
Der Hauptvorteil des vorgestellten High-Q-Matchings (QL>1000) besteht darin, dass die Gesamteffizienz des RF Harvesting Systems gegenüber einem Low-Q-Matching (QL<200) erhöht wird. Ein weiterer Vorteil resultiert aus dem Sachverhalt, dass durch eine Erhöhung der belasteten Güte die Spannungsamplitude am Eingang der Gleichrichterschaltung vergrößert wird. Dadurch ist unter Umständen keine zusätzliche Spannungsvervielfachung, z. B. in Form einer Ladungspumpe oder einer Spannungskaskade, notwendig, was die Schaltungstopologie des RF Energy Harvesting Systems vereinfacht.
1.5 Nachteile des High-Q-Matchings
Durch die Impedanzanpassung mit einem SAW-Resonator erhöht sich der belastete Gütefaktor Q des Gesamtsystems. Je größer die belastete Güte ist, umso schmalbandiger ist die Anpassung, denn der belastete Gütefaktor Q kann aus der Frequenz f (auch Mittenfrequenz genannt) bezogen auf die Bandbreite B festgelegt werden als:
(18) 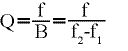
Die Bandbreite B ist hier der Frequenzbereich, an dessen Grenzen sich der Eingangsreflexionsfaktor am Eingang der Anpassungsschaltung um den linearen Faktor 0,707 gegenüber dem Extremwert geändert hat, im logarithmischen Maß entspricht dies ungefähr -3 dB. Die obere Grenzfrequenz wird als f2 und die untere Grenzfrequenz als f1 bezeichnet.
Ein weiteres Problem ist, dass die Serien- und Parallelresonanzfrequenz bei Resonatoren oft eng beieinander liegen (einige hundert kHz). Dadurch ist der Wertebereich der Induktivität, die man mit dem Resonator realisieren kann, ebenfalls begrenzt.
2. Methoden
Verschiedene High-Q und Low-Q Anpassungsnetzwerke werden in nächsten Kapitel theoretisch analysiert und simuliert. Für die Simulationen werden die Programme Qucs (Quite Universal Circuit Simulator) und Keysight ADS (Advanced Design System) verwendet. Die verschiedenen Anpassungsnetzwerke sollen bei 868 MHz (Frequenzband, welches für das vorgestellte RF Energy Harvesting System verwendet worden ist) miteinander bezüglich Gütefaktor, Effizienz und Breitbandigkeit verglichen werden.
3. Ergebnisse
Für die High-Q-Anpassung im 868 MHz Band wird ein SAW-Resonator (Epcos R958) mit folgenden Parametern verwendet:

Die Streuparameter des SAW-Resonators werden mithilfe von Qucs simuliert. Streuparameter (abgekürzt S-Parameter) dienen zur Charakterisierung des Verhaltens elektrischer Komponenten und Netzwerken im Klein- und Großsignalverhalten mittels Wellengrößen.
Das Ersatzschaltbild des verwendeten SAW-Resonators inklusive Ein- und Ausgangsanschluss ist in der folgenden Abbildung dargestellt.
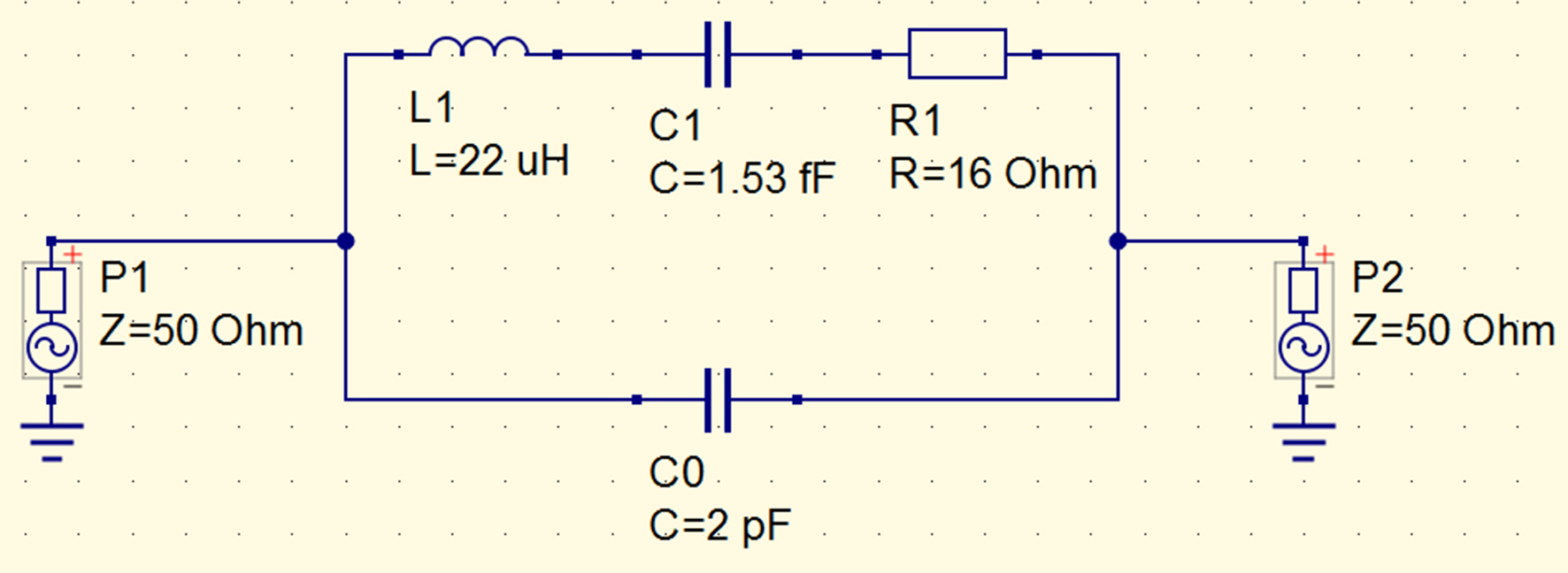
Abb. 8: Ersatzschaltbild des verwendeten SAW-Resonators
Die Abhängigkeit des Eingangsreflexionsfaktors und des Vorwärtstransmissionsfaktors von der Eingangsfrequenz (siehe Abbildung 9) zeigt, dass die Fehlanpassung bei der Serienresonanzfrequenz am geringsten ist und bei der Parallelresonanz wie erwartet am höchsten. Die Eingangsfrequenz wird zwischen den beiden Werten gewählt, z. B. bei 867,6 MHz. Aufgrund der Bidirektionalität des SAW-Resonators entspricht der Frequenzverlauf des S11-Parameters dem des S22-Parameters und der S21-Parameter dem des S12-Parameters. Die S12- und S21-Parameter sind deshalb nicht in der Abbildung 9 dargestellt. Die Simulation des Blindwiderstands des SAW-Resonators wird in Abbildung 10 gezeigt.
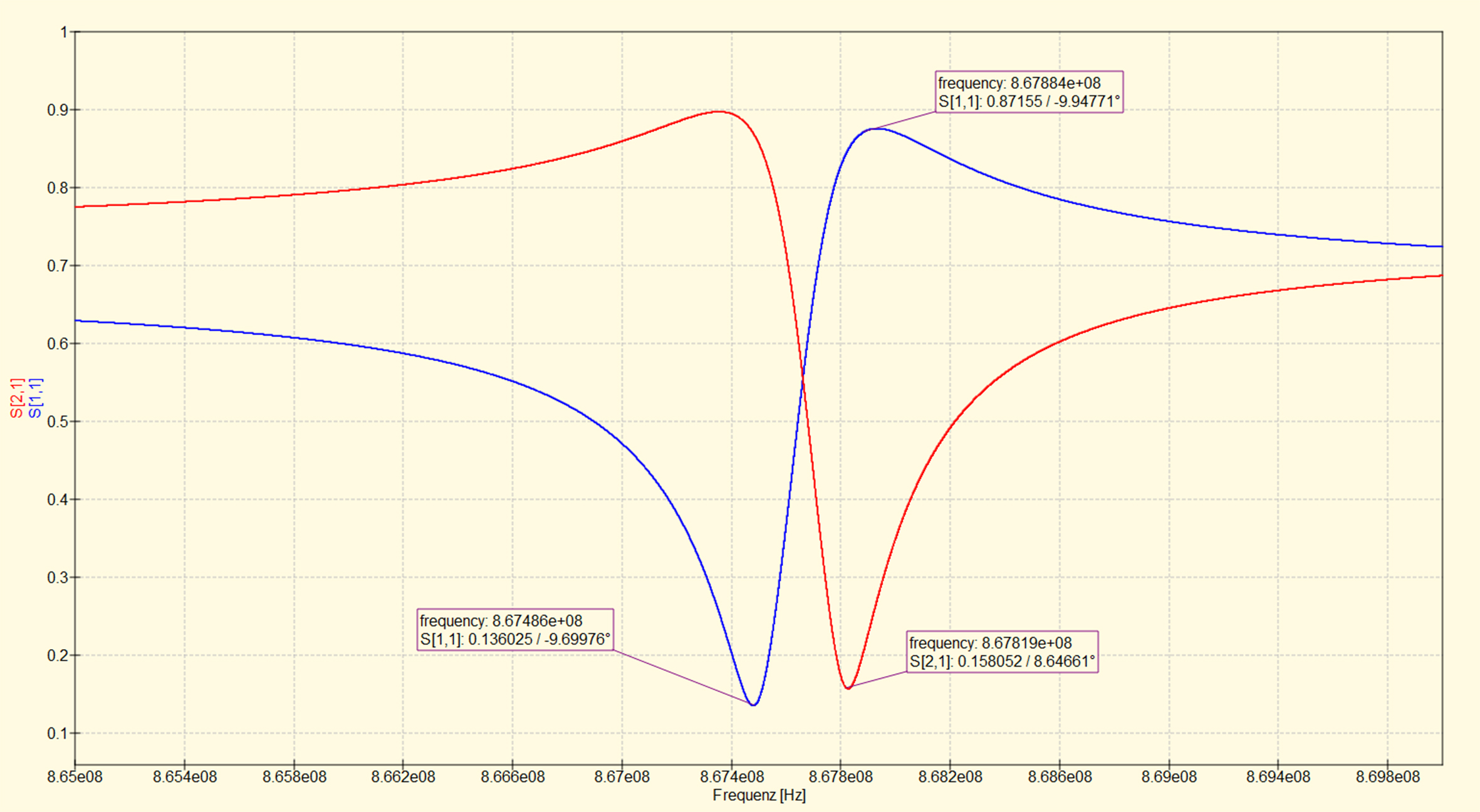
Abb. 9: Eingangsreflexionsfaktor und Vorwärtstransmissionsfaktor des SAW-Resonators in Abhängigkeit von der Eingangsfrequenz
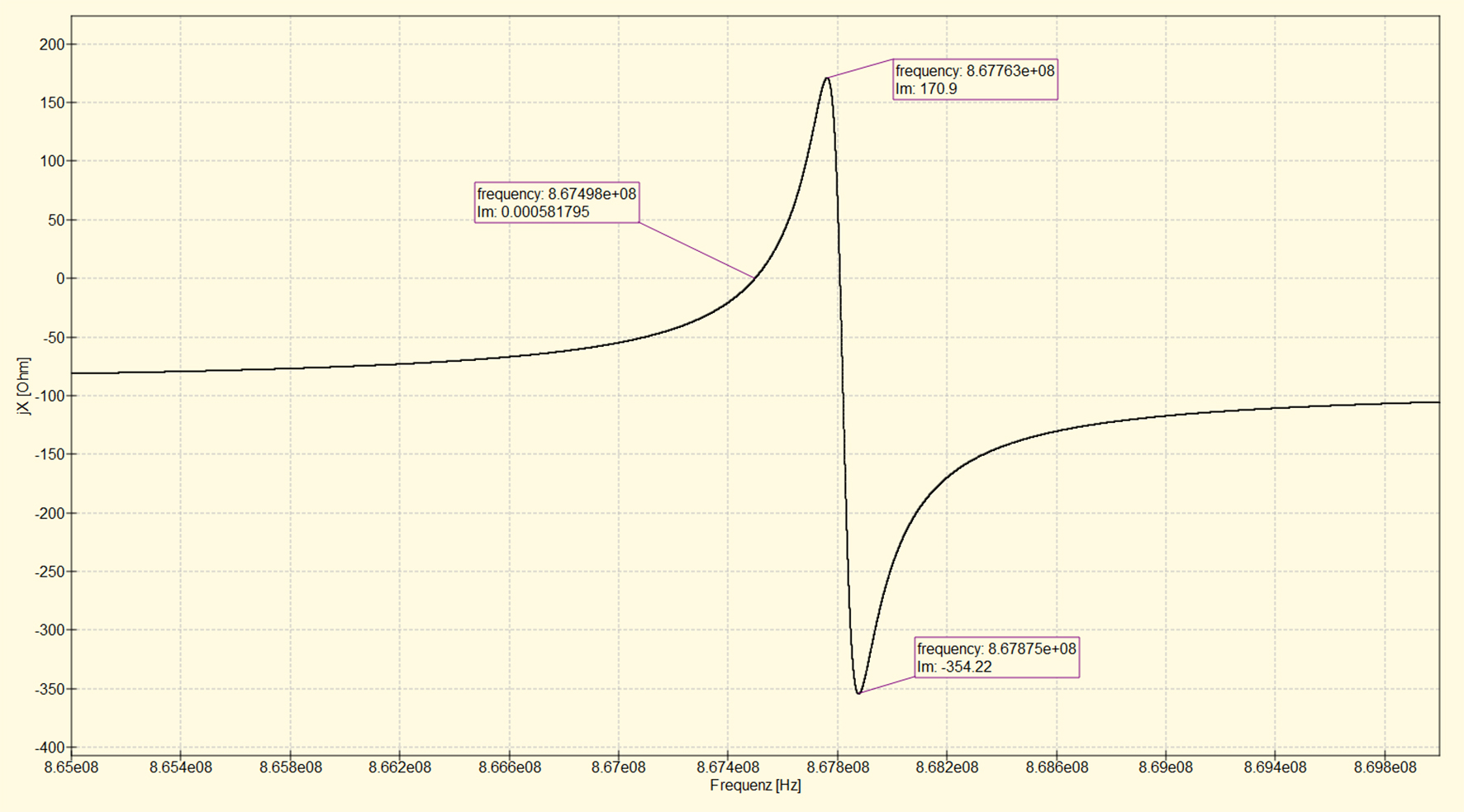
Abb. 10: Blindwiderstand des SAW-Resonators in Abhängigkeit von der Eingangsfrequenz
Wie zu erwarten ist, ist bei der Serienresonanzfrequenz, die etwa bei 867,5 MHz liegt, der Blindwiderstand null. Der Blindwiderstand ist bei der Parallelresonanzfrequenz am höchsten. Zwischen der Serien- und Parallelresonanzfrequenz ist der Blindwiderstand positiv. Deswegen erscheint der SAW-Resonator in diesem Bereich nach außen hin rein induktiv. Bei Frequenzen, die über der Parallelresonanzfrequenz liegen, hat der Resonator ein kapazitives Verhalten. Der induktive Bereich (867,5 MHz – 867,7 MHz) liegt teilweise innerhalb des Frequenzbandes, in dem man laut der Bundesnetzagentur eine Leistung von 2 Watt (ERP) abstrahlen darf (865,6 MHz – 867,6 MHz). Aus diesem Grund eignet sich der Resonator für RF Energy Harvesting Anwendungen.
Im Folgenden werden zwei Gleichrichterschaltungen mit High-Q und Low-Q Anpassung miteinander verglichen. Die Gleichrichterschaltung ist eine 7-fach kaskadierte Greinacher-Schaltung mit einem Speicherkondensator und einem Lastwiderstand. Auf ein Power-Management wird der Einfachheit halber verzichtet. Die Einflüsse von Substrat und Leitungen werden bei den nachfolgenden Simulationen vernachlässigt.
Der Schaltplan des niedergütigen Harvesters (siehe Abbildung 11) zeigt das Ersatzschaltbild für die Empfangsantenne, welches aus einem Signalgenerator mit Innenwiderstand besteht, die kaskadierte Greinacher-Schaltung, den Speicherkondensator und den Lastwiderstand. Das Anpassungsnetzwerk besteht aus einer Induktivität und einer Kapazität in L-Topologie.
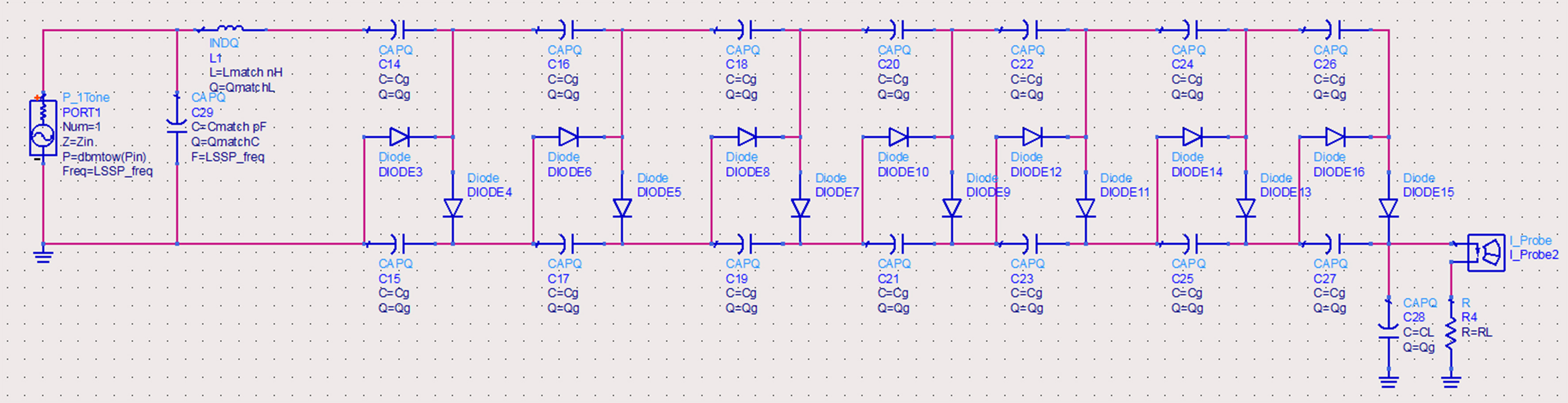
Abb. 11: Schaltplan der Harvester-Testschaltung (Low-Q)
Bei der Simulation werden die folgenden Parameter verwendet:

Bei der verwendeten Diode handelt es sich um die Schottky-Diode HSMS-285x von Avago Technologies.
Aus dem Verlauf des Eingangsreflexionsfaktors in Abhängigkeit von der Frequenz (siehe Abbildung 12) ergibt sich ein unbelasteter Gütefaktor von 0,64. Bei der Arbeitsfrequenz hat der Eingangsreflexionsfaktor den Wert 0,7 %. Aus der Gleichung 18 errechnet sich eine Bandbreite von 1,36 GHz.
Der Eingangsreflexionsfaktor in Abhängigkeit von der Eingangsleistung (siehe Abbildung 13) zeigt, dass der Fehlanpassungsgrad unter der angepassten Leistung (-8,2 dBm) sehr hoch ist (etwa 70 %). Das bedeutet, dass bei geringen Eingangsleistungen (kleiner als 30 dBm) 70 % dieser Leistung reflektiert wird.
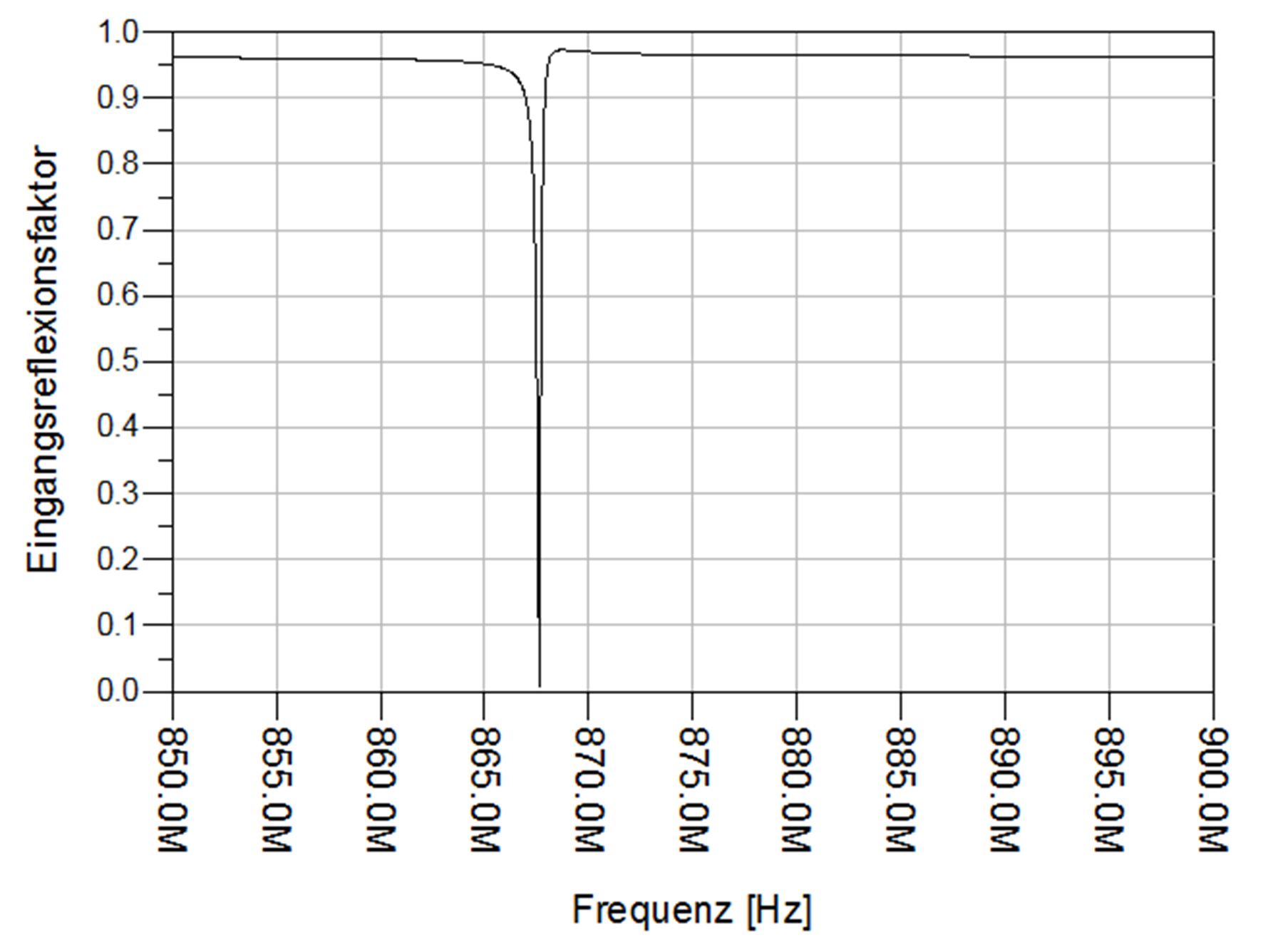
Abb. 12: Eingangsreflexionsfaktor in Abhängigkeit von der Frequenz (Low-Q)
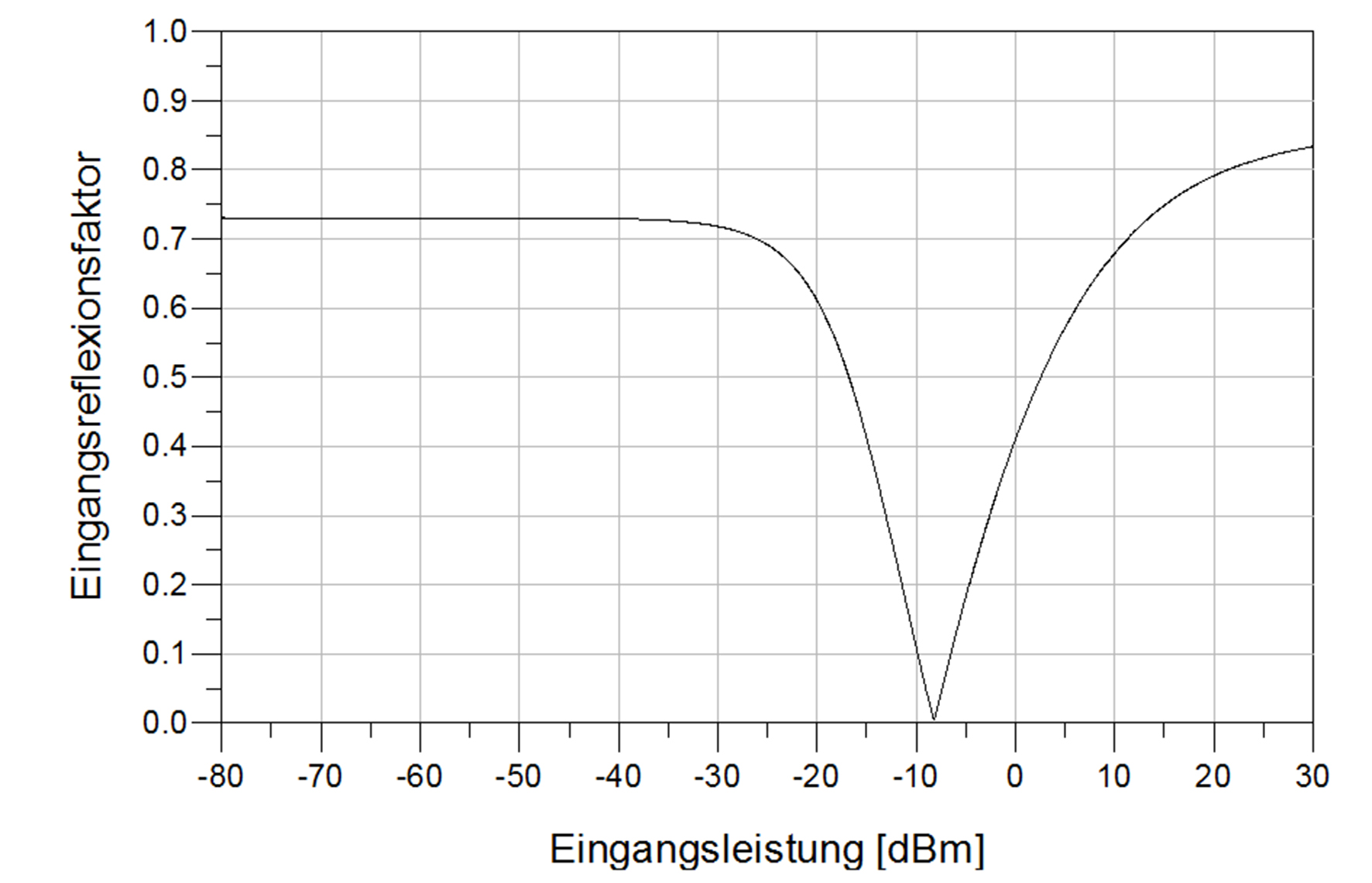
Abb. 13: Eingangsreflexionsfaktor in Abhängigkeit von der Eingangsleistung (Low-Q)
Der Schaltplan der hochgütigen Testschaltung ist in der nachfolgenden Abbildung dargestellt.
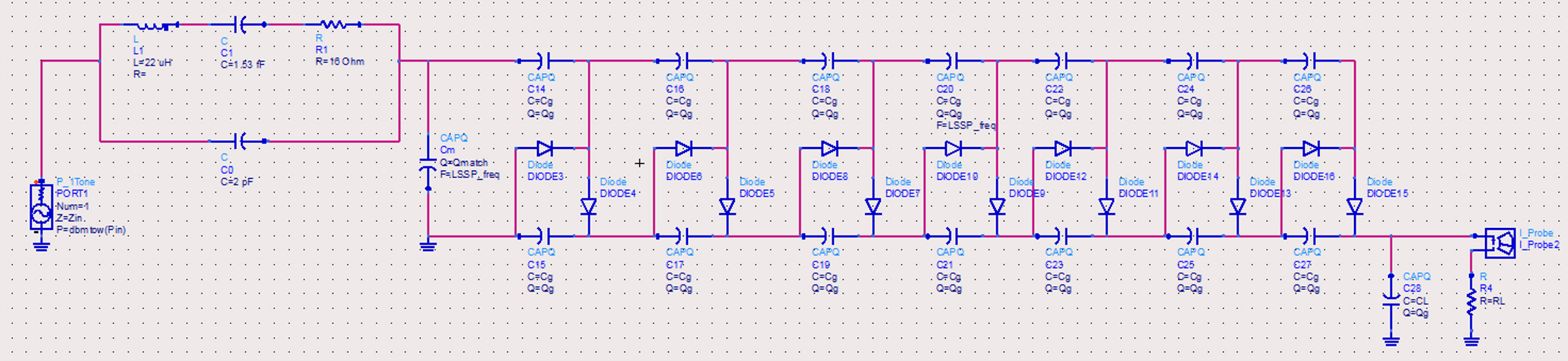
Abb. 14: Schaltplan der Harvester-Testschaltung (High-Q)
Die Testschaltung unterscheidet sich von der in Abbildung 11 dadurch, dass anstatt der Induktivität ein SAW-Resonator verwendet worden ist und dass die Komponentengüte der Kapazität im Anpassungsnetzwerk 5000 beträgt. Alle restlichen Parameter bleiben aus Gründen der Vergleichbarkeit identisch. Aus dem Verlauf des Eingangsreflexionsfaktors in Abhängigkeit von der Frequenz (siehe Abbildung 15) ergibt sich ein belasteter Gütefaktor von 2892 und bei der Arbeitsfrequenz von 867,6 MHz für S11 ein Wert von 0,7 %. Die Simulation des Eingangsreflexionsfaktors in Abhängigkeit von der Eingangsleistung (siehe Abbildung 16) zeigt, dass die Fehlanpassung bei geringeren Eingangsleistungen (kleiner als -20 dBm) kleiner ist (ca. 12 %) als bei der niedergütigen Testschaltung.

Abb. 15: Eingangsreflexionsfaktor in Abhängigkeit von der Frequenz (High-Q)
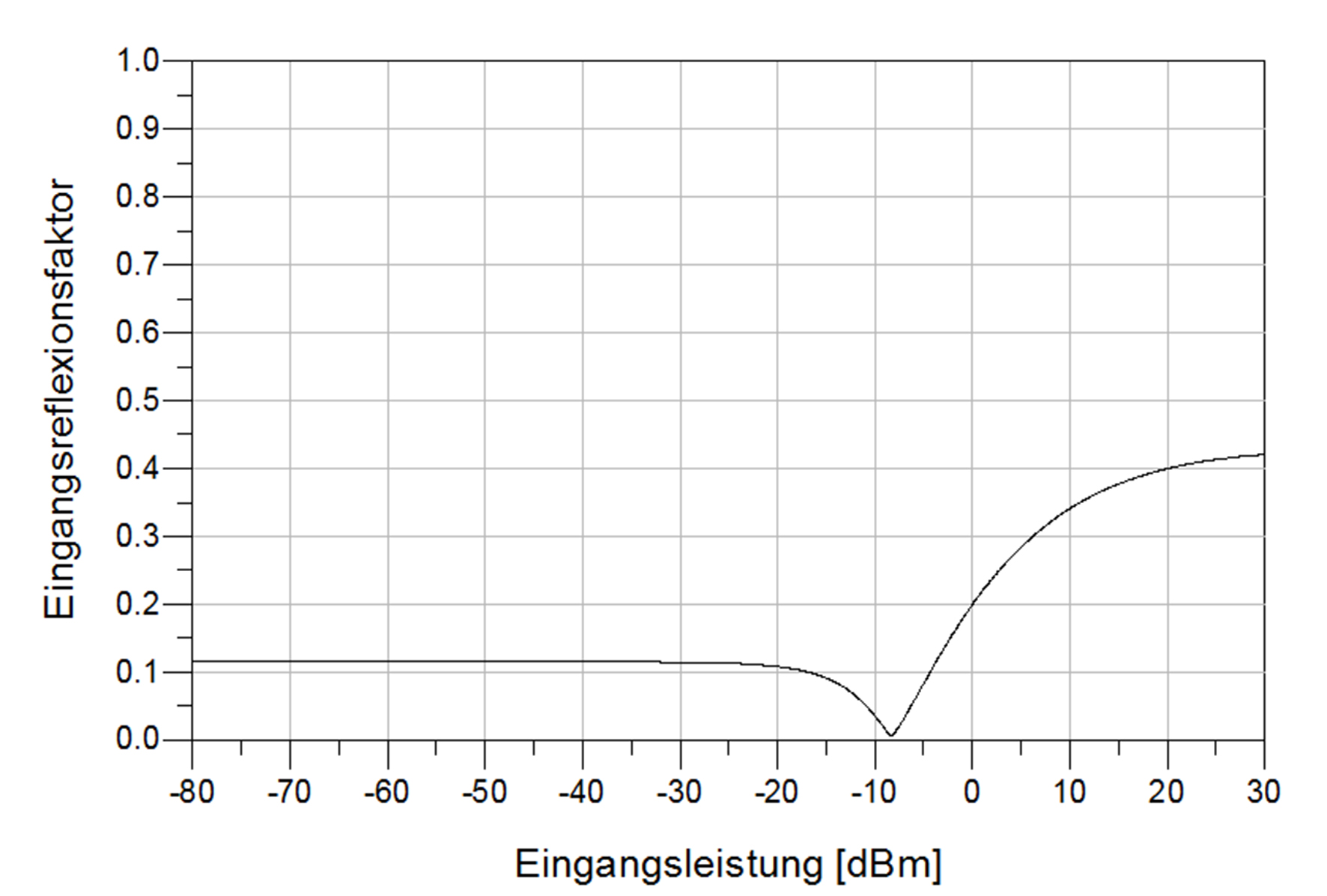
Abb. 16: Eingangsreflexionsfaktor in Abhängigkeit von der Eingangsleistung (High-Q)
Die Effizienz eines Anpassungsnetzwerk hängt neben der Spannungstransformation Vp/VS von der Spulengüte ab. Durch eine Kaskadierung der L-Anpassungsnetzwerke erhöht sich bei einer zunehmenden Spannungstransformation die Effizienz des Anpassungsnetzwerks. Abbildung 17 zeigt beispielhaft die Effizienz eines L-Anpassungsnetzwerks in Abhängigkeit von der Spulengüte QL und verschiedenen Kaskadierungsstufen bei einer Spannungstransformation von 4.
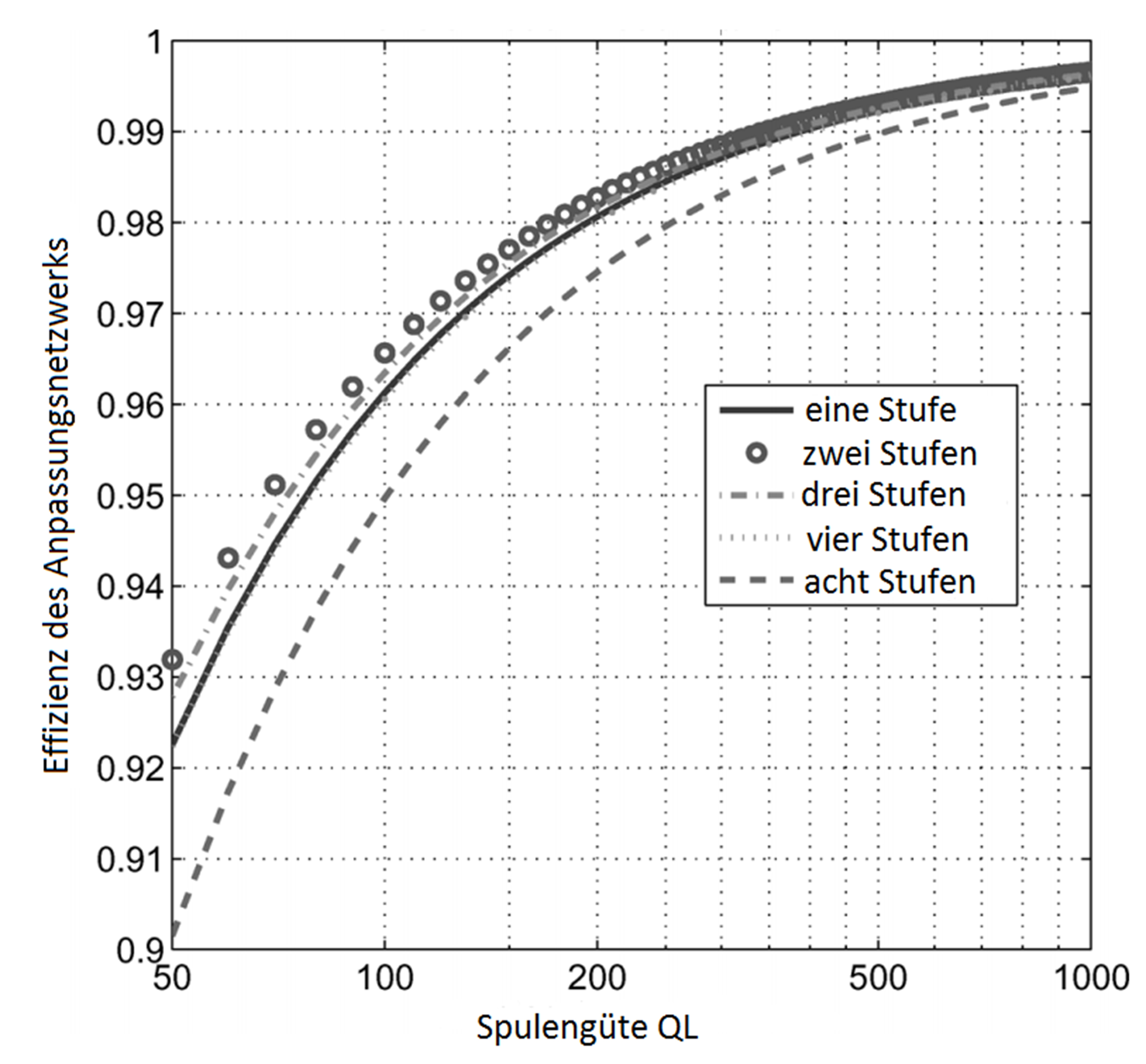
Abb. 17: Effizienz in Abhängigkeit von der Spulengüte [4]
4. Diskussion und Ausblick
In dieser Arbeit wurde gezeigt, dass durch die Verwendung eines SAW-Resonators als induktives Element hoher Güte in einer L-Anpassungsschaltung die Effizienz der Anpassung erhöht werden kann. Aufgrund der Simulationsergebnisse, welche in den Abbildungen 13 und 16 dargestellt sind, zeigt sich, dass bei hochgütigen Anpassungssystemen der Eingangsreflexionsfaktor bei sich veränderter Eingangsleistung nicht so stark erhöht wird wie bei Systemen niedriger Güte, wodurch weniger Leistung am Eingang reflektiert wird. Für Energy Harvesting Anwendungen sollte deswegen eine möglichst hohe Systemgüte angestrebt werden.
Der Grund dafür ist, dass die Eingangsleistungen bei derartigen Anwendungen stark variieren können, wenn beispielsweise die Distanz zwischen Sender und Empfänger geändert wird oder unterschiedliche Dämpfungen im Übertragungsweg auftreten.
Um die Simulationsergebnisse messtechnisch verifizieren zu können, sollen die simulierten Testschaltungen zukünftig aufgebaut und analysiert werden.
5. Erklärung zu möglichen Interessenkonflikten
Die Autoren erklären, dass in Zusammenhang mit der vorliegenden Arbeit keinerlei Interessenskonflikt besteht.
6. Literatur
[1] K. Dembowski, Energy Harvesting für die Mikroelektronik, VDE Verlag, Berlin, 2011.
[2] C. Merz, G. Kupris and M. Niedernhuber, Speisung von energieautarken Sensorsystemen durch elektromagnetische Felder, 1. Elektronik Power Management Congress, 2014.
[3] Mindan, Bai; Hong, Liang, The Analysis of Impedance Matching Problem in RF Circuit Design, 2010 International Forum on Information, pp. 350–353.
[4] Han, Y.; Perreault, D. J., Analysis and Design of High Efficiency Matching Networks, IEEE Transactions on Power Electronics, vol. 21, no. 5, September 2006, pp. 1484-1491.
[5] C. Bowick, J. Blyler, C. Ajluni, RF Circuit Design, Newnes, 2nd edition, 2007.
[6] T. Ungan, X. Le Polozec, W. Walker, L.M. Reindl, RF energy harvesting design using high Q resonators, 2009 Cavtat, Croatia Proc. of IMWS 2009, IEEE MTT-S International Microwave Workshop on Wireless Sensing,
Local Positioning, and RFID, Seiten: 1 – 4.
[7] B. Neubig und W. Briese, Das große Quarzkochbuch, Franzis Verlag GmbH, 2000.

Christian Merz, M.Sc.
Christian Merz hat an der Technischen Hochschule Deggendorf (THD) ein Bachelor- und Masterstudium im Studiengang Elektro- und Informationstechnik (Schwerpunkte Nachrichtentechnik und Elektronische und Nachrichtentechnische Systeme) absolviert. Derzeit ist er Doktorand an der THD in Kooperation mit der Technischen Universität Ilmenau. Seine Forschungsinteressen liegen in den Bereichen Drahtlose Energieübertragung, Hochfrequenztechnik und Energy Harvesting. Der Autor hat bisher 5 Publikationen zum Thema RF Energy Harvesting veröffentlicht und forscht derzeit an Methoden zur Effizienzsteigerung von Energy Harvesting Schaltungen.
Christian Merz has earned a bachelor and a master degree in electrical and information technology (focus on communication engineering and electronic and communication engineering systems) at Deggendorf Institute of Technology. At the moment he is writing his dissertation in cooperation with Ilmenau University. His research interests lie in the fields of wireless energy transmission, high-frequency technology and energy harvesting. Christian Merz has already published 5 articles on RF energy harvesting and is currently working on methods to improve the efficiency of energy harvesting circuits.
Kontakt / Contact:

Prof. Dr.-Ing. Gerald Kupris
Prof. Dr.-Ing. Gerald Kupris ist seit 2009 Professor an der Technischen Hochschule Deggendorf und arbeitet auf dem Gebiet des Entwurfs eingebetteter Systeme. Seine berufliche Laufbahn begann er 1989 als Entwicklungsingenieur. 1994 schloss er seine Promotion im Bereich der Elektronik an der Technischen Universität Ilmenau ab und begann als Applikationsingenieur zu arbeiten. Zwischen 1998 und 2009 war er Senior Field Application Engineer bei Motorola und Freescale Semiconductor, dabei lag sein Schwerpunkt auf Projekten mit Mikrocontrollern und drahtloser Kommunikation.
Prof. Dr. Gerald Kupris has been a professor for Embedded Systems Design at Deggendorf Institute of Technology since 2009. He started his career in 1989 as a design engineer. In 1994, he received his Ph.D. in electronics from the Technical University of Ilmenau and started to work as an application engineer. Between 1998 and 2009 he has been a Senior Field Application Engineer at Motorola and Freescale Semiconductor, focusing on projects with microcontrollers and wireless connectivity.
Kontakt / Contact:
